CAPITOLO 4
“Case study”: il metodo del sistema aggiunto esteso
4.1 Il modello
L’ambiente software implementato per l’addestramento delle reti neurali feed-forward che
è stato precedentemente descritto, sarà qui utilizzato e dove necessario ampliato per
realizzare un’architettura di controllo ottimo a N stadi, capace di risolvere il problema
“reale” ora descritto.
Si vuole progettare un dispositivo intelligente o controllore capace di guidare, attraverso
un numero N fissato di stadi temporali, un qualunque sistema dinamico in modo tale che il suo
vettore di stato minimizzi una certa funzione di costo J.
Se il problema è posto in un contesto non deterministico, caratterizzato dalla presenza
di variabili stocastiche che agiscono da disturbo sul sistema dinamico e che rendono il suo stato
non perfettamente prevedibile, la strategia per il controllo ottimo ha una qualche forma di
feedback che dipende dal vettore di stato corrente
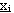 , altrimenti questa condizione non sarebbe
essenziale (contesto deterministico), ma è bene che sia comunque soddisfatta, per essere
in grado di fronteggiare il caso in cui dovessero verificarsi scostamenti imprevisti dalla
traiettoria “deterministica”.
, altrimenti questa condizione non sarebbe
essenziale (contesto deterministico), ma è bene che sia comunque soddisfatta, per essere
in grado di fronteggiare il caso in cui dovessero verificarsi scostamenti imprevisti dalla
traiettoria “deterministica”.
Nel caso deterministico, in assenza di disturbi sullo stato, si considera il sistema dinamico
tempo-discreto e in genere non lineare
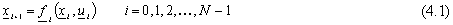
dove 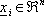 è il vettore di stato del sistema
dinamico tempo-variante,
è il vettore di stato del sistema
dinamico tempo-variante, 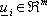 quello dei
controlli. La funzione di costo, non necessariamente quadratica, è invece definita da
quello dei
controlli. La funzione di costo, non necessariamente quadratica, è invece definita da

dove 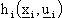 è il costo di transizione
da uno stato al successivo, mentre
è il costo di transizione
da uno stato al successivo, mentre 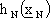 rappresenta il costo sullo stato stato finale, esprimibile in
rappresenta il costo sullo stato stato finale, esprimibile in
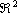 ad esempio quale distanza dall’obiettivo
finale
ad esempio quale distanza dall’obiettivo
finale

con 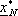 stato finale che si desidera raggiungere.
stato finale che si desidera raggiungere.
Il problema così formulato si traduce nel trovare l’insieme dei controlli ottimi
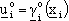 (feedback sullo stato, “anello chiuso”)
con i = 0, 1, ..., N-1, tale da minimizzare il costo J.
(feedback sullo stato, “anello chiuso”)
con i = 0, 1, ..., N-1, tale da minimizzare il costo J.
Nel caso non deterministico, invece, il sistema dinamico e la funzione di costo assumono
rispettivamente le seguenti forme:
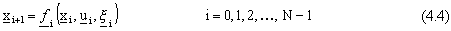

dove, in genere, 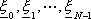 è una sequenza di vettori
aleatori misurabili con densità di probabilità
è una sequenza di vettori
aleatori misurabili con densità di probabilità 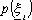 nota, che rappresenta il disturbo sul sistema.
nota, che rappresenta il disturbo sul sistema.
Sotto queste ipotesi, si deve ora determinare l’insieme delle funzioni ottime decisionali
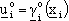 , con i = 0, 1, ..., N-1, tale da
minimizzare il valor medio del costo J.
, con i = 0, 1, ..., N-1, tale da
minimizzare il valor medio del costo J.
Quando il sistema dinamico presenta delle non linearità e/o la funzione di costo è non quadratica,
i metodi tradizionali, quali la programmazione dinamica, sono di non facile applicazione perché
richiedono generalmente una discretizzazione dello spazio degli stati, che presenta una crescita
esponenziale con le dimensioni del vettore di stato (maledizione della dimensionalità).
Inoltre, se 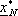 appartiene ad un compatto
appartiene ad un compatto
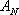 , anziché essere un unico stato finale
desiderato, risolvere il problema con la programmazione dinamica equivale a definire più problemi,
uno per ogni possibile
, anziché essere un unico stato finale
desiderato, risolvere il problema con la programmazione dinamica equivale a definire più problemi,
uno per ogni possibile 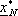 obiettivo. Tutto ciò
si traduce in un’enorme complessità di calcolo, accompagnata da un’ingente richiesta di memoria
per memorizzare gli stati con i rispettivi controlli.
obiettivo. Tutto ciò
si traduce in un’enorme complessità di calcolo, accompagnata da un’ingente richiesta di memoria
per memorizzare gli stati con i rispettivi controlli.
Un’alternativa alla programmazione dinamica, che consente di superare questi limiti, consiste
nell’assegnare alla strategia di controllo la forma
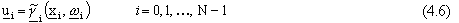
dove 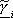 ha la struttura di rete approssimante
(nell’esempio qui trattato una multilayer feed-forward neural network) e
ha la struttura di rete approssimante
(nell’esempio qui trattato una multilayer feed-forward neural network) e
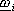 il rispettivo vettore dei parametri liberi
da ottimizzare, ovvero il vettore dei pesi.
il rispettivo vettore dei parametri liberi
da ottimizzare, ovvero il vettore dei pesi.
La struttura del controllore neurale tempo-invariante potrebbe essere quella rappresentata,
rispettivamente nel caso deterministico o non deterministico, in figura 4-1 o in fgura 4-2:
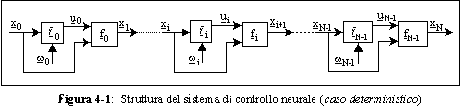
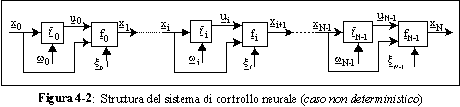
Le singole reti neurali feed-forward 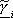 ,
solitamente scelte con la medesima struttura, hanno il compito di generare il controllo
,
solitamente scelte con la medesima struttura, hanno il compito di generare il controllo
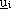 che viene passato al sistema dinamico,
ovvero alla funzione di stato, per generare il nuovo vettore di stato
che viene passato al sistema dinamico,
ovvero alla funzione di stato, per generare il nuovo vettore di stato
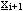 .
.
Una tale scelta implementativa per il controllore conduce quindi verso un problema di
programmazione non lineare (risolubile ad esempio col metodo del gradiente), del tipo

o, per il caso non deterministico,

una volta definito 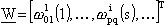 come il vettore di
tutti i pesi delle singole reti, dove
come il vettore di
tutti i pesi delle singole reti, dove 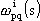 rappresenta il peso del neurone q appartenente al livello s della rete
i sull’uscita p del livello s-1.
rappresenta il peso del neurone q appartenente al livello s della rete
i sull’uscita p del livello s-1.
Se vogliamo partire invece da un qualsiasi stato iniziale
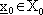 , possiamo modificare il costo nella
seguente maniera:
, possiamo modificare il costo nella
seguente maniera:
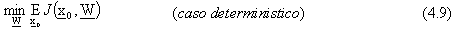
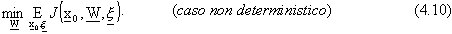
Per il problema in questione, considerando un contesto deterministico, l’algoritmo del gradiente
può così essere espresso nello spazio dei pesi,
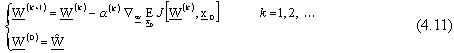
dove k denota il passo di iterazione dell’algorimo, mentre
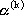 è una funzione che definisce la lunghezza
del passo di discesa, decrescente con k per assicurare la convergenza al punto ottimo
è una funzione che definisce la lunghezza
del passo di discesa, decrescente con k per assicurare la convergenza al punto ottimo
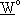 e solitamente espressa come:
e solitamente espressa come:

con 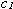 e
e
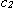 costanti da determinare.
costanti da determinare.
Per la complessità computazionale della media  ,
si preferisce ricorrere alla tecnica del “gradiente stocastico” e calcolare pertanto
,
si preferisce ricorrere alla tecnica del “gradiente stocastico” e calcolare pertanto
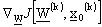 , estraendo ad ogni passo di iterazione
k il vettore
, estraendo ad ogni passo di iterazione
k il vettore 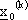 dal dominio compatto
dal dominio compatto
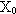 , secondo l’opportuna distribuzione di
probabilità.
, secondo l’opportuna distribuzione di
probabilità.
Sotto queste ipotesi, l’algoritmo di aggiornamento per il vettore dei pesi dell’intera sequenza
di reti neurali diventa:
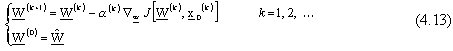
L’operatore gradiente può essere espresso anche come vettore colonna delle derivate parziali,
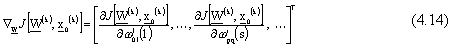
realizzando in questo modo il concetto del calcolo distribuito nel quale ogni peso viene
aggiornato solo sulla base di informazioni locali.
Prima di procedere nel calcolo delle derivate parziali, è utile definire due variabili che giocano
un ruolo fondamentale nello sviluppo dell’algoritmo di apprendimento (l’indice k verrà
omesso per alleggerire la notazione)


dove i = 0, 1, ..., N-1 rappresenta la rete i-esima del “treno”, s = 1, ...,
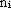 il livello s della rete i
e q = 1, ...,
il livello s della rete i
e q = 1, ..., 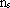 il suo
corrispondente neurone q.
il suo
corrispondente neurone q.
Con tali definizioni, applicando la regola della back-propagation alle N reti neurali che
costituiscono il modello, si ottiene:

dove le 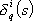 possono essere calcolate
ricorsivamente dal seguente sistema
possono essere calcolate
ricorsivamente dal seguente sistema
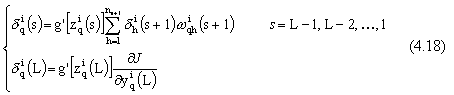
con L che rappresenta il numero dei livelli della rete i.
Nel sistema (4.18) g’ rappresenta la derivata della funzione di attivazione
che caratterizza il neurone q del livello s. Ovviamente, le derivate parziali
della funzione di costo J rispetto ai bias
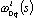 nella (4.17) sono ottenute impostando
il corrispondente ingresso q a 1.
nella (4.17) sono ottenute impostando
il corrispondente ingresso q a 1.
Prima di risolvere le equazioni della back-propagation (4.18) per la generazione delle
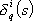 , è necessario determinare le componenti
q del vettore
, è necessario determinare le componenti
q del vettore 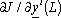 , ovvero le derivate
parziali di J rispetto all’uscita q dell’ultimo livello della rete i,
attraverso
, ovvero le derivate
parziali di J rispetto all’uscita q dell’ultimo livello della rete i,
attraverso
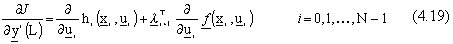
dove le 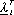 sono ottenute anch’esse
ricorsivamente dal sistema:
sono ottenute anch’esse
ricorsivamente dal sistema:
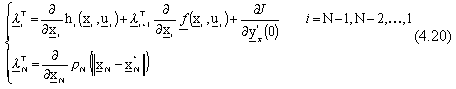
con

In questo modo il calcolo ricorsivo delle 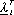 è riconducibile alla teoria del controllo ottimo in N-stadi, con l’aggiuna di
è riconducibile alla teoria del controllo ottimo in N-stadi, con l’aggiuna di
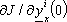 che permette di cosiderare l’introduzione
delle reti neurali.
che permette di cosiderare l’introduzione
delle reti neurali.
Di qui deriva il nome di metodo del sistema aggiunto esteso, e per una descrizione più
dettagliata si rimanda, per esempio, a [5], [6] e [7].
L’algoritmo di apprendimento si compone dunque di due “fasi” che procedono in maniera alternata
durante ogni passo:
1) “fase forward” dove, una volta estratto casualmente il vettore di stato
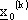 da
da
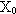 , sono generate la sequenza dei controlli e
la traiettoria dello stato, che dipendono da
, sono generate la sequenza dei controlli e
la traiettoria dello stato, che dipendono da 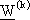
2) “fase backward” in cui, una volta calcolate le variabili
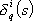 e
e
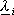 a ritroso, viene determinato il gradiente
a ritroso, viene determinato il gradiente
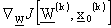 che consente di eseguire un passo di
discesa e di trovare così
che consente di eseguire un passo di
discesa e di trovare così 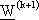
In un contesto non deterministico, dove lo stato è perturbato dalla presenza delle
variabili aleatorie 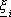 , il problema di
programmazione non lineare si trasforma nel determinare la sequenza delle leggi o funzioni
ottime decisionali
, il problema di
programmazione non lineare si trasforma nel determinare la sequenza delle leggi o funzioni
ottime decisionali
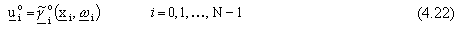
in grado di minimizzare il valor medio di J rispetto a
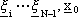 , ovvero:
, ovvero:

dove

L’algoritmo del gradiente diventa
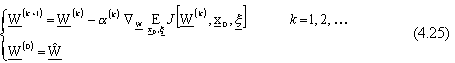
e ricorrendo poi all’approssimazione stocastica:
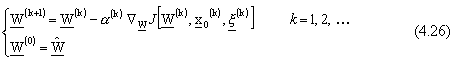
Procedendo quindi con tutte le considerazioni viste per il caso deterministico, ma ricordando
che nella funzione di stato e in quella di costo esiste una dipendenza dal vettore
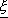 dei disturbi aleatori sul sistema, si
ottiene un algoritmo di apprendimento analogo al precedente, con la sola differenza che nella
fase forward devono essere estratte anche le componenti
dei disturbi aleatori sul sistema, si
ottiene un algoritmo di apprendimento analogo al precedente, con la sola differenza che nella
fase forward devono essere estratte anche le componenti
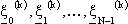 .
.
4.2 Tempi di sviluppo
Con tempo di sviluppo intendiamo il lavoro necessario alla realizzazione del modello
completo e funzionante, a partire dal progetto e dall’analisi dei requisiti fino ad ottenere,
attraverso successive fasi di implementazione e collaudo, un codice privo di errori, quindi
traducibile in forma eseguibile.
Nel nostro caso lo sviluppo in Matlab/C di un’archittettura per il controllo ottimo a N stadi
si è basato sulle funzioni già implementate (descritte nel terzo capitolo) per la costruzione
e l’addestramento delle reti neurali feed-forward, mantenendo quindi lo stesso “formalismo” e
ampliando, ove necessario, il modello con l’aggiunta di nuove strutture dati, nuove funzioni
e in qualche caso di nuove librerie.
Fin dalle prime fasi, cioè dalla realizzazione della struttura dati del “metodo del sistema
aggiunto esteso”, l’implementazione in Matlab si è rilevata essere più veloce e compatta
rispetto alla sua complementare C.
Va subito sottolineato che, in questa fase e nelle successive, l’aspetto fondamentale che ha
consentito di velocizzare enormemente lo sviluppo del modello in Matlab è dovuto alla possibilità
offerta da questo ambiente all’utente di operare sui dati in maniera istantanea. Le funzioni poi,
oltre a poter naturalmente ricevere diverse variabili in input, possono anche restituire più
output: ad entrambi si può accedere semplicemente dalla riga di comando.
Nella “versione C” del modello, oltre all’uso delle variabili puntatore per gestire gli oggetti
più strutturati (partendo da vettori, matrici, insiemi di vettori o di matrici, neuroni, reti
neurali, sino ad arrivare al “treno” stesso), che hanno permesso un controllo totale sui dati
accompagnato però da un notevole rallentamento nello sviluppo delle procedure, si è dovuto
“inventare” un metodo per consentire l’accesso a tali variabili.
Si è scelto così di gestire il flusso di input/output attraverso l’uso di files di testo con
opportuno formato e, in maniera più “classica”, mediante l’input da tastiera o l’output su
schermo.
Files di testo sono quindi utilizzati come vere e proprie variabili per contenere ad esempio
i parametri della simulazione, la struttura del “treno” e delle singole reti che lo compongono,
i pesi del “treno”, il numero di passi e la durata in secondi dell’addestramento, le traiettorie
di prova per il sistema.
Ovviamente questa soluzione ha rallentato non di poco la realizzazione del nostro modello: per
ogni “tipologia” di file di testo, dopo averne stabilito un formato compatibile con le variabili
in esso contenute, si è reso necessario definire funzioni di accesso per la lettura e la scrittura
delle informazioni, oltre a quelle già strettamente necessarie alla codifica del modello.
Ritornando ora all’implementazione della struttura dati che caratterizza il modello in esame,
si può notare come essa debba senz’altro includere la sequenza delle singole reti neurali
feed-forward e il corrispondente numero.
In Matlab è stato possibile definire la sequenza delle N reti feed-forward semplicemente come
cell-array, dove la prima cella contiene il numero di reti neurali che compongono la struttura,
mentre a tutte le altre sono assegnate le singole reti, ciascuna ottenuta dopo una chiamata alla
funzione buildnet o caricata da file per mezzo del comando load.
Le reti non sono vincolate ad avere la stessa struttura, anche se in molti problemi ciò si
verifica: la funzione costruttore buildtrain, oltre a eseguire l’assegnazione rete
neurale/cella, si limita infatti a verificare che la dimensione dell’uscita di ogni singola
rete sia uguale a quella dell’ingresso della sucessiva, per poi inizializzarne i pesi nel
dominio specificato.
In C il “treno” ha una struttura leggermente più complessa perchè in essa compare, oltre al
numero delle reti e alla lista dinamicamente lincata delle reti stesse, l’insieme dei vettori
di stato del sistema.
Una volta allocato lo spazio di memoria sufficiente con alloc_train, occorre per i
motivi precedentemente elencati utilizzare load_train che legge da file le proprietà
delle struttura (numero di reti, numero di ingressi, numero di livelli, numero di neuroni e
tipo di funzione di attivazione per livello) e che è pertanto caratterizzata dal seguente
prototipo (contenuto in tr_kern.h):
void load_train (const char *train_file, TRAIN *qt)
dove qt rappresenta un puntatore alla struttura “treno” precedentemente allocata, mentre
train_file è il nome del file di testo che ne contiene le caratteristiche.
A questo punto la funzione init_train può caricare i pesi di un precedente
addestramento dal file dei pesi o estrarli nuovamente. Essa riceve perciò in ingresso il nome
del file dei pesi, una variabile booleana che indica quando utilizzare tale file, un puntatore
alle strutture dati “simulazione” (descritta nel seguito) e “treno”, come possiamo notare dal
prototipo
void init_train (const char *weight_file, BOOLEAN initflag, SIMULATION *sim, TRAIN *qt)
Si è così giunti ad avere due realizzazioni parallele per il “treno”, ora utilizzabili per
definire e risolvere il problema del controllo ottimo a N stadi.
In Matlab, l’ottimizzazione dei pesi del “treno” viene affettuata all’interno di optimize
con l’algoritimo della back-propagation specificato sul modello, con un richiamo esplicito alle
funzioni forward e backward già implementate sulle singole reti neurali.
I parametri specifici dell’addestramento sono passati come input alla funzione.
In C si è dovuto dapprima definire la nuova struttura simulazione, in grado di contenere le
caratteristiche dell’addestramento, fra le quali
· numero di passi
· range degli ingressi, dei rumori sul sistema e dei pesi iniziali
· costanti 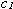 e
e
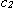 per definire il passo di discesa
per definire il passo di discesa
· soglia di arresto sul costo J
· intervallo di memorizzazione
· numero ingressi di test su cui valutare J
quindi realizzare le funzioni info_simul e load_simul per accedervi, oltre al
costruttore salloc e al distruttore de_salloc.
Detto ciò, è stato possibile implementare il main train.c con il corrispondente file
eseguibile in cui, una volta costruito e inizializzato il modello attraverso le informazioni
sull’addestramento (contenute nel file della simulazione) e sul “treno” (caricate dal file
contenente la struttura del “treno” e da quello dei pesi), viene eseguita la fase di addestramento
per mezzo di ripetute chiamate alle funzioni forward_train e backward_train che
realizzano sull’intera sequenza di reti le omonime fasi della back-propagation.
Queste ultime due funzioni, importantissime perchè semplificano l’aggiornamento dei pesi delle
singole reti che costituiscono il “treno” (in Matlab tutto avviene all’interno di optimize),
sono caratterizzate dai prototipi:
void forward_train (TRAIN *qt, VET_DB in, MATR_DB rs) ;
void backward_train (TRAIN *qt, DOP_REALE k, VET_DB xstar, MATR_DB rs) ;
dove in è il vettore degli ingressi alla struttura “treno”, rs la matrice dei rumori sul sistema,
k la lunghezza del passo di discesa e xstar lo stato finale obiettivo.
Per quanto riguarda la simulazione e la rappresentazione delle traiettorie, in Matlab tutto è
affidato alla sola funzione goaltrain che estrae una serie di stati iniziali e di
disturbi sul sistema, li passa al “treno” precedentemente addestrato e ne disegna quindi
l’evoluzione dinamica.
In C, al contrario, un secondo main strike.c si preoccupa di simulare alcune traiettorie
e di salvarle su file di testo, lasciando quindi alla funzione matlab draw_trajectory
il compito di visualizzarle graficamente.
4.3 Facilità di scrittura/debugging
La facilità di scrittura e di debugging, oltre a condizionare ulteriormente i tempi di sviluppo
del modello, influisce sulle successive fasi di manutenzione o di riuso di una parte più o meno
significativa del codice.
Nel modello in esame Matlab, grazie al suo tipo base (l’array) e alla possibilità di esprimere
i problemi con le rispettive soluzioni in una notazione matematica familiare, ha consentito di
sviluppare procedure snelle e compatte: ad esempio l’algoritmo di addestramento del “treno”
basato sulla back-propagation, che compare all’interno della funzione optimize, è stato
codificato molto velocemente. In C, al contrario, l’uso continuo di cicli for e delle
variabili puntatore ha reso il processo di definizione assai più lento, portando inoltre alla
realizzazione delle funzioni forward_train e backward_train.
Nel realizzare l’implementazione in C del modello, si è dovuto inoltre “sdoppiare” alcune
procedure per rendere il software compatibile con entrambi gli ambienti UNIX e MS-DOS, al fine
di ottenerne la massima portabilità.
Terminate le fasi di sviluppo e di collaudo del codice, non è stato così possibile né eseguire
una comune compilazione né tanto meno creare programmi eseguibili su entrambe le piattaforme,
in quanto sono rimaste due sostanziali differenze in merito a:
· chiamate a sistema (per la pulizia dello schermo, ad esempio, UNIX utilizza la funzione
clear, mentre l’MS-DOS cls)
· estrazione casuale dei numeri (il generatore di numeri casuali viene inizializzato in
UNIX con srand48 e in MS-DOS con srand, mentre per l’estrazione sono impiegate
rispettivamente drand48 e rand).
Tutto ciò ha condizionato notevolmente anche la fase di debugging, volta a individuare e eliminare
gli eventuali errori di sintassi o in run-time.
Lo strumento del break point invece, offerto a supporto dell’interprete Matlab e che
consente l’esecuzione passo-passo delle funzioni, ha velocizzato di molto le operazioni di
collaudo sugli m-file.
4.4 Facilità d'uso
La facilità d’uso si raggiunge quando più persone, anche con conoscenze molto diverse, sono in
grado di imparare facilmente come utilizzare un determinato software grazie alla sua semplicità.
Naturalmente, a seconda del tipo di applicazione, sono diversi i fattori che possono condizionare
questa importante caratteristica.
Per quanto riguarda il modello del controllore neurale in esame, gli aspetti da tenere in
considerazione per valutarne la semplicità di accesso da parte dell’utente sono i seguenti:
· costruzione del modello
· inizializzazione del modello
· aggiornamento del modello
· aggiornamento delle specifiche di addestramento
· aggiornamento del sistema (funzione di stato, funzione di costo, …)
· simulazione delle traiettorie del sistema
· rappresentazione grafica.
Per quanto riguarda “l’utilizzo in sè” del modello, l’ambiente Matlab offre una maggiore
flessibiltà rispetto al C, essendo possibile richiamare dal prompt dei comandi le seguenti
funzioni (definite nei rispettivi M-file) per eseguire manualmente tutte le operazioni di
costruzione, inizializzazione e addestramento del “treno” di reti:
1) buildtrain costruisce e inizializza il “treno” a partire dalla sequenza ordinata delle
reti, tutte ottenibili da una precedente chiamata alla funzione buildnet, e dal range iniziale dei
pesi, una volta verificato che il numero di ingressi di ogni rete corrisponda al numero di uscite
della rete precedente, come è qui mostrato dalla chiamata:
train = buildtrain (0.5, net_1, net_2)
che costruisce il “treno” composto nell’ordine da net_1 e net_2, inizializzandone i pesi in
[-0.5,0.5];
2) optimize addestra il “treno” e aggiorna conseguentemente i pesi dell’intera struttura,
salvandola poi anche su file. Riceve come input il “treno” già inizializzato, il dominio degli
ingressi e dei disturbi sul sistema, lo stato finale obiettivo, il numero dei passi di
addestramento, le costanti c1 e c2 per definire il passo di discesa, la soglia di arresto,
restituendo alla fine il “treno” aggiornato. Visualizza poi graficamente l’andamento del costo e
salva infine su un file di testo la durata in secondi del solo processo di addestramento.
Una tipica chiamata alla funzione optimize può essere perciò:
[new_train] = optimize (train, Xo, CSI, xnstar, npassi, soglia, c1, c2)
3) goaltrain simula e visualizza graficamente le traiettorie del sistema. Prende in
input il “treno” addestrato, il range degli ingressi e dei disturbi, il numero di passi di
addestramento precedentemente effettuati sul “treno” e il numero di simulazioni da compiere,
come è possibile capire dal seguente esempio:
goaltrain (train, [-1 1;-1 1], [-.2 .2;-.2 .2], [0;0], 1000, 20)
Offrendo Matlab funzioni di accesso al file system molto potenti, quali load e
save, è doveroso inoltre sottolineare quanto sia immediato salvare o caricare da file
la variabile “treno” per riprendere nuovi addestramenti o per esegure successive fasi di
simulazione “on line”.
Con il C è stato invece possibile realizzare due eseguibili in ambienti MS-DOS/UNIX, fatto
estremamente importante perché le funzioni Matlab appena elencate hanno bisogno dell’interprete
per poter essere eseguite.
In particolare, l’esegubile train.exe o train, rispettivamente per gli ambienti
MS-DOS o UNIX, che compie l’addestramento e l’aggiornamento dei pesi del “treno”, necessita di
ricevere sulla riga di comando i nomi di tre file di testo opportunamente formattati, come appare
evidente dalla tipica chiamata
train simul_file train_file weights_file
dove:
· simul_file è il file che contiene tutti i parametri caratteristici della simulazione, quelli
cioè precedentemente elencati per la funzione Matlab addestra, escluso la struttura del “treno”
· train_file è il file nel quale si trova descritta la struttura del “treno”, ovvero il numero
delle reti e, per ognuna di esse, il numero di ingressi, il numero dei livelli, il numero di
neuroni e il tipo di funzione di attivazione per livello
· weights_file è il file in cui sono memorizzati, livello per livello, i pesi di tutte le reti
neurali del “treno”, ovvero il suo stato attuale.
Sul file dei pesi si verificano operazioni sia in lettura che in scrittura, essendo questo
responsabile di mantenere aggiornato lo stato sinaptico del “treno”. Ai precedenti file si
aggiungono inoltre quello del numero dei passi effettivi di addestramento e quello della sua
durata temporale, utilizzati per una successiva chiamata di train o per la simulazione
delle traiettorie, ai quali l’utente non fa però direttamente riferimento.
L’eseguibile strike.exe o strike, invece, verifica l’efficacia dell’addestramento
simulando alcune traiettorie di prova per il sistema, dopo aver appreso la struttura aggiornata del
“treno” e le informazioni sulla simulazione dai primi tre parametri che vengono passati al
programma e che sono gli stessi precedentemente descritti per train.exe.
In più occorre specificare il nome del file sul quale si vuole vengano memorizzate, in formato
testuale, le traiettorie simulate e naturalmente il numero di queste ultime, per una successiva
rappresentazione grafica. Quindi la chiamata dell’eseguibile strike assume la seguente forma:
strike simul_file train_file weights_file trajectory_file number_of_test
Per quanto riguarda invece l’aggiornamento del modello o delle specifiche di addestramento, si
nota un’impostazione completamente diversa nelle due implementazioni, che porta la versione Matlab
ad essere nettamente più veloce sotto questo punto di vista.
Qui, come già analizzato, modificare la struttura del “treno”, delle singole reti o dei parametri
dell’addestramento, equivale a richiamare semplicemente le funzioni buildtrain,
buildnet o optimize rispettivamente, specificando gli opportuni parametri.
Nella corrispondente versione in C, dove si è scelto di gestire il flusso input/output dei due
eseguibili train e strike attraverso files di testo opportunamente formattati,
occorre invece modificare manualmente i files della simulazione o del trenino, attraverso un
qualsiasi editor di testi.
Per entrambe le implementazioni l’aggiornamento del sistema equivale alla modifica della funzione
di stato del sistema, della funzione di costo e delle rispettive derivate parziali: ovviamente
nella “versione C” del modello si rende necessaria una ri-compilazione dei sorgenti.
Infine, per la rappresentazione grafica delle traiettorie del sistema, aspetto molto importante
perché da esso è possibile verificare la bontà dell’addestramento, si è fatto ricorso a funzioni
Matlab per entrambe le implementazioni, dal momento che questo ambiente offre routine grafiche
potenti e soprattutto di facile/veloce utilizzo.
Ciò ha condizionato la fase di simulazione delle traiettorie, comportando anche in questo caso un
diverso approccio al problema.
In Matlab, come abbiamo avuto già modo di constatare, simulazione e rappresentazione grafica delle
traiettorie sono eseguite contemporaneamente all’interno della funzione goaltrain che,
dopo aver estratto casualmente un dato numero di ingressi e di disturbi sul sistema, esegue la
fase forward attraverso le reti del “treno” e quindi disegnata la corrispondente traiettoria.
Al contrario in C queste due operazioni sono attuate in momenti diversi: l’eseguibile
strike.exe simula le traiettorie del sistema e le salva su un file di testo, quindi la
funzione matlab draw_trajectory legge il file delle traiettorie e le rappresenta
graficamente.
4.5 Librerie a disposizione
Saranno qui presentate e brevemente elencate alcune delle funzioni a disposizione dell’utente per
la codifica del problema del controllo ottimo a N stadi. Come si è avuto già occasione di
osservare nei paragrafi precedenti, Matlab consente di codificare il modello “istantaneamente”
solo attraverso:
· buildtrain (costruzione e inizializzazione del modello)
· optimize (aggiornamento dei pesi della struttura)
· goaltrain (simulazione e rappresentazione grafica delle traiettorie del sistema)
oltre naturalmente alle funzioni per la definizione del sistema dinamico e per la gestione delle
singole reti neurali.
In C, invece, le funzioni implementate per il “treno” comprendono un ampio “software di contorno”,
composto da procedure anche non strettamente connesse al problema in esame, ma pur sempre
indispensabili al modello, che ha permesso di realizzare vere e proprie librerie, fra le quali
ricordiamo:
· tr_mem.h (contenente le funzioni per l’allocazione dinamica del “treno”, come il
costruttore alloc_train e il distruttore de_alloc_train, o della simulazione,
quali salloc e de_salloc)
· tr_kern.h (in cui si possono trovare le funzioni per la definizione e l’inizializzazione
della struttura “treno” come load_train, init_train e load_weights_train,
o quelle per salvare il suo stato e le traiettorie simulate per il sistema quali save_train
e save_trajectory, o quelle infine dedicate all’addestramento come forward_train
e backward_train)
· tr_sys.h (in cui compaiono accanto a funzioni di utilità, come ad esempio per
l’inizializzazione casuale degli elementi di vettori e matrici, vet_d_init e
matr_d_init, le procedure per definire il sistema dinamico o la funzione di costo, quali
dinamic_system o cost_function, e le loro rispettive derivate parziali)
4.6 Efficienza computazionale
Con efficienza computazionale intendiamo la capacità di un programma di svolgere in tempi
ragionevoli i compiti per cui è stato realizzato, usando il minor numero di risorse.
Nel modello in esame, le N reti neurali feed-forward che costituiscono il “treno”, dopo una o più
serie di passi addestramento, devono essere in grado di condurre il sistema in uno stato finale
desiderato, a partire da un qualunque stato iniziale appartenente al dominio del problema.
Per quanto riguarda l’uso delle risorse si può subito notare come l’implementazione in C del
modello “treno” ricorra in maniera assai pesante all’uso del file system: ciò rallenta non di
poco le fasi di aquisizione dei dati e di restituzione degli outputs.
Tuttavia questo ritardo non condiziona il funzionamento dell’intero sistema e quindi, dal momento
che per entrambe le implementazioni è stato scelto l’algoritmo della back-propagation quale metodo
per l’addestramento delle reti neurali, risulta particolarmente interessante confrontare i tempi
di apprendimento nelle due implementazioni.
Gli esempi che seguono sono stati ottenuti su un processore Pentium III a 500 MHz: a scanso di
equivoci e per una corretta interpretazione dei risultati, occorre quindi considerare il rapporto
fra i tempi, anzichè i tempi effettivi.
Si consideri, ad esempio, il sistema dinamico tempo-discreto definito dalla seguente funzione
di stato:
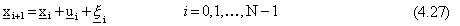
dove 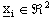 è il vettore di stato con
è il vettore di stato con
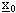 appartenente al dominio del problema
(la dimensione è 2 solo per motivi di rappresentazione grafica),
appartenente al dominio del problema
(la dimensione è 2 solo per motivi di rappresentazione grafica),
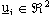 il controllo generato dalla rete
i-esima a 2 strati del trenino, mentre
il controllo generato dalla rete
i-esima a 2 strati del trenino, mentre
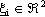 rappresenta il disturbo che agisce sul
sistema, estratto casualmente secondo una distribuzione uniforme specificata di volta in volta
(così come
rappresenta il disturbo che agisce sul
sistema, estratto casualmente secondo una distribuzione uniforme specificata di volta in volta
(così come 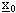 ).
).
Definendo ora la funzione di costo
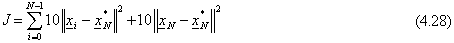
con  , si può inizialmente addestrare il
“treno” per condurre il sistema da un solo stato inziale
, si può inizialmente addestrare il
“treno” per condurre il sistema da un solo stato inziale
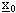 verso lo stato obbiettivo (N è il numero
di reti che compongono il “treno” e rappresenta il numero di passi intermedi consentito fra lo
stato iniziale e quello finale).
verso lo stato obbiettivo (N è il numero
di reti che compongono il “treno” e rappresenta il numero di passi intermedi consentito fra lo
stato iniziale e quello finale).
Se N = 1, il sistema dovrà essere in grado di raggiungere lo stato obiettivo in un solo “balzo”.
Dalla figura 4-4 e dalle successive si vede come per un singolo punto occorrano pochissimi passi
di addestramento:
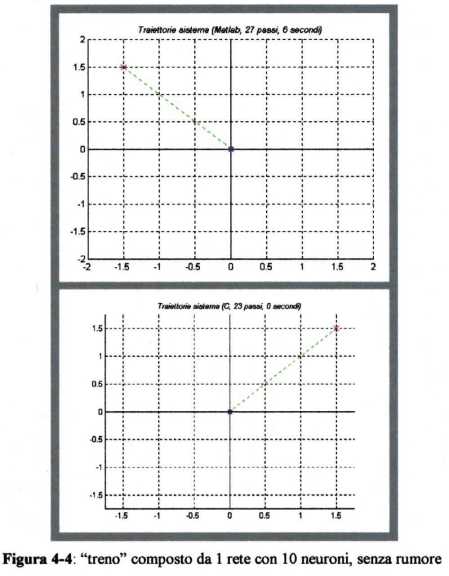
Se N = 2, il sistema ha a disposizione due “istanti temporali” per raggiungere l’obiettivo,
ma poichè nella funzione J (4.28) non compare alcun costo sul controllo, l’origine
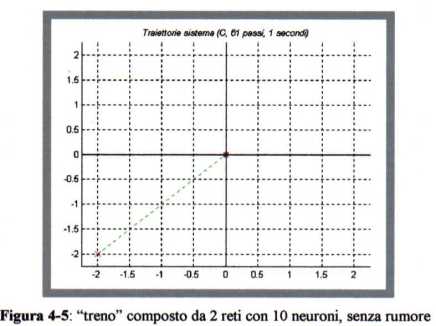
viene centrata subito col primo balzo, come si vede nella figura 4-5:
Quanto visto, soprattutto per i sistemi dinamici a più stadi, porta a considerare, all’interno
della funzione J da minimizzare, costi di transizione che dipendano più o meno fortemente
dal controllo 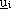 , in modo da ottenere
traiettorie più regolari e meglio distribuite “nel tempo”.
, in modo da ottenere
traiettorie più regolari e meglio distribuite “nel tempo”.
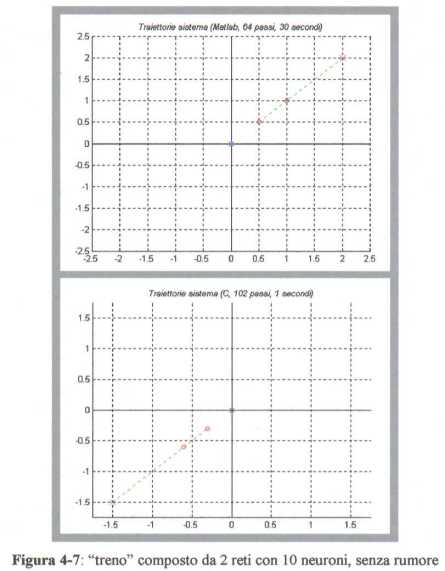
Considerando così la funzione di costo (4.29) per N = 2,
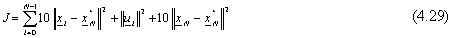
si ottiene il seguente comportamento:
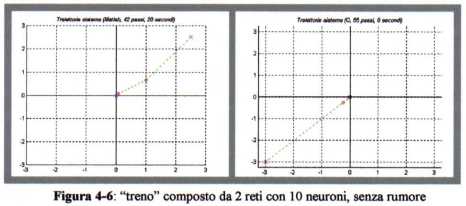
mentre, se definiamo
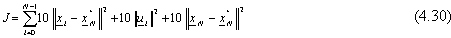
sempre con N = 2, si ha:
Il costo sul controllo che, ad esempio, nel caso reale di una sonda spaziale potrebbe
essere proporzionale alla quantità di carburante necessaria ad eseguire una determinata manovra,
condiziona quindi la lunghezza dei singoli passi che andranno a costitituire la traiettoria
del sistema.
Il costo sullo stato finale e sugli stati intermedi penalizza invece i punti della
traiettoria lontani dallo stato finale desiderato.
Per questo motivo, negli esempi che seguono, si è scelto di considerare quale funzione di costo
J da minimizzare l’espressione:
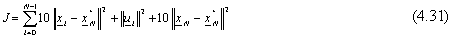
essendo questa un buon compromesso soprattutto nei casi in cui N > 1, quando cioè il sistema
dinamico evolve attraverso più stadi temporali.
Ovviamente le considerazioni fatte sinora valgono comunque se ci troviamo in uno dei seguenti
casi:
· lo stato finale desiderato non coincide con l’origine
· il “treno” viene addestrato su un insieme compatto di stati iniziali, quello cioè specificato
dal dominio del problema (sinora avevamo considerato un solo stato iniziale)
· sono presenti variabili aleatorie che agiscono da disturbo sul sistema.
Negli ultimi due casi saranno necessari molti passi di addestramento in più rispetto a quelli
per il singolo punto iniziale.
Va però ricordato che, grazie alle buone proprietà di generalizzazione delle reti neurali, il
sistema è in grado di rispondere in maniera accettabile anche ad uno “stimolo” esterno al
dominio del problema.
Ad esempio, se 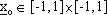 , N = 1 e sul sistema non
agisce alcun disturbo, già con 500 passi di addestramento si ottiene un buon risultato,
, N = 1 e sul sistema non
agisce alcun disturbo, già con 500 passi di addestramento si ottiene un buon risultato,
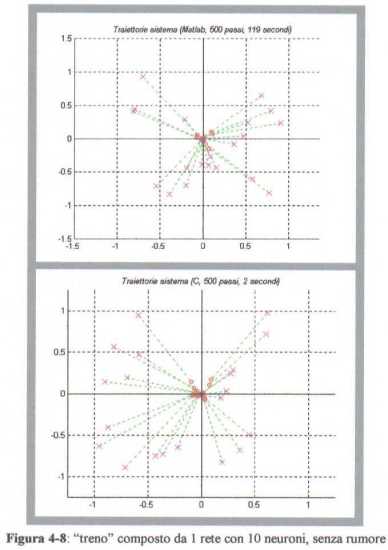
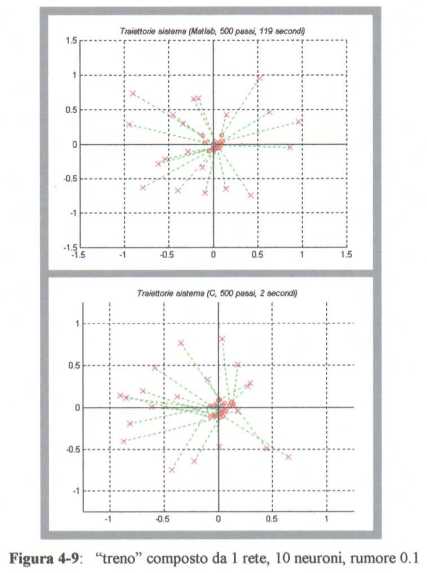
mentre, se sul sistema agisce un disturbo 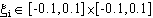 ,
la traiettoria può “deviare” dall’obiettivo, come mostrato in figura 4-9.
,
la traiettoria può “deviare” dall’obiettivo, come mostrato in figura 4-9.
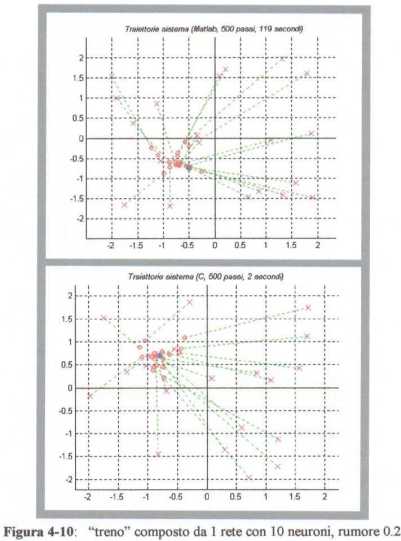
Se invece 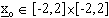 e soprattutto
e soprattutto
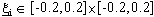 , lo stato finale desiderato è raggiunto
con maggiore difficoltà (figura 4-10).
, lo stato finale desiderato è raggiunto
con maggiore difficoltà (figura 4-10).
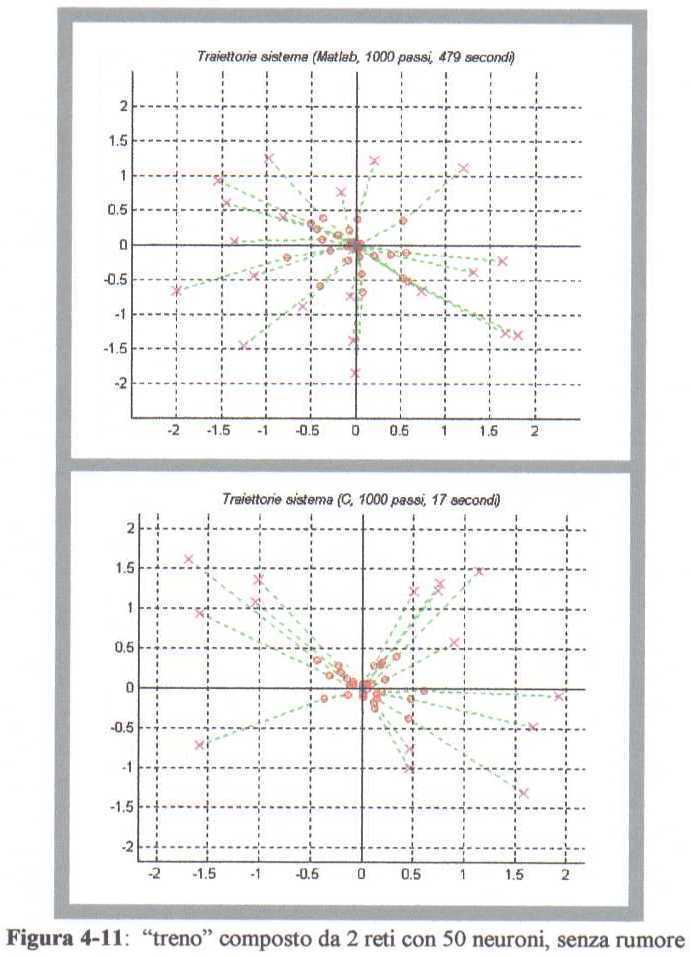
Se il sistema dispone di 2 stadi temporali, in un contesto deterministico con
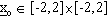 e con 50 neuroni al primo livello di ogni
rete, otteniamo il comportamento di figura 4-11.
e con 50 neuroni al primo livello di ogni
rete, otteniamo il comportamento di figura 4-11.
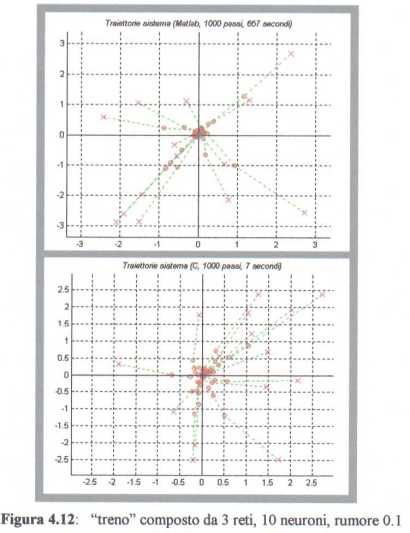
Con N = 3, invece, la traiettoria tende a “distribuirsi” su 3 passi, comportamento intuibile
dalla figura 4-12.
4.7 Conclusioni e sviluppi futuri
Nei paragrafi precedenti, una volta definito “in astratto” il problema del controllo ottimo a N
stadi e dedotta una strategia basata sulle reti neurali per la sua soluzione, ovvero il
metodo del sistema aggiunto esteso, si è pervenuti alla corrispondente realizzazione
“su elaboratore”, attraverso l’implementazione di due modelli paralleli in Matlab e in C
(capitolo 3), capaci di soddisfarne le specifiche.
Considerando gli “ambienti software”
precedentemente costruiti per la gestione delle reti neurali, ci siamo subito resi conto di
quanto le strutture dati e le relative metodologie di accesso offerte dai due linguaggi di
programmazione avrebbero condizionato l’evoluzione del modello.
Fin dalle prime fasi di sviluppo, infatti, sono state necessarie scelte implementative differenti,
anche in campi “banali” come quello dell’aquisizione dei dati, che hanno fortemente “indebolito”
le speranze di mantere quel parallelismo auspicato inizialmente.
Nonostante ciò abbiamo individuato alcune caratteristiche “oggettive”, riconducibili in parte
a quelle qualità esterne che un prodotto software dovrebbe possedere (correttezza, robustezza,
estendibilità, riusabilità, portabilità, efficienza computazionale, facilità d’uso), che
consentono di effettuare un confronto fra le due implemementazioni, quali:
· tempi di sviluppo
· facilità di scrittura/debugging
· facilità d’uso
· librerie a disposizione
· efficienza computazionale.
Ritornando quindi al nostro obiettivo principale, che era quello di sviluppare un modello non solo
rispondente alle specifiche del problema (correttezza), ma anche capace di sposare l’efficienza di
calcolo con la facilità di utilizzo da parte dell’utente, alla luce di quanto osservato possiamo
trarre alcune considerazioni, valide certamente per il modello in esame, ma di carattere generale
in alcuni casi.
· La realizzazione in Matlab del nostro modello si è rilevata assai veloce, principalmente
a causa della presenza di strutture dati molto efficienti (array e cell-array), della possibilità
di operare “direttamente” sui dati e di accedere “istantaneamente” al file system. I fattori che
invece hanno determinato l’allungamento dei tempi di sviluppo in C sono stati: definizione di
strutture dati elementari (vettori, matrici), allocazione dinamica della memoria, aquisizione dei
dati tramite files di testo.
· Anche la facilità di scrittura/debbuging ha influito notevolmente sui tempi implementativi,
favorendo ulteriormente la “versione in Matlab” del modello. Questo ambiente, per esempio, ha
consentito non solo una formulazione pseudo-matematica e quindi compatta degli algoritmi di
ddestramento, cosa non permessa dal C per l’uso delle variabili puntatore e per l’“esplosione”
del codice, ma anche la “scomposizione” del modello in poche funzioni base. Inoltre, la necessità
in C di rendere il software compatibile su entrambe le piattaforme UNIX e MS-DOS ha causato lo
“sdoppiamento” di alcune procedure, rallentando ulteriormente la fase di scrittura/debugging del
codice.
· In Matlab è possibile gestire l’intero modello attraverso un numero molto limitato di funzioni,
che consentono un accesso diretto alle strutture dati principali (rete neurale, “treno”), ma che
necessitano dell’interprete Matlab per poter essere chiamate. In C, al contrario, i due eseguibili
realizzati sono meno “flessibili”, in quanto gestiscono l’accesso ai dati attraverso files di
testo, che devono essere disponibili all’atto della chiamata. Ad essi l’utente può comunque
accedere attraverso un qualsiasi editor di testi, per aggiornare la struttura del “treno”,
i parametri di addestramento o anche i singoli pesi.
· In C si è reso necessario lo sviluppo di un ampio software di supporto al modello, che ha
portato alla realizzazione di alcune librerie utilizzabili anche in contesti non strettamente
connessi al problema in esame.
· La rappresentazione delle traiettorie è gestita in entrambe le implementazioni da funzioni
Matlab, in quanto questo ambiente offre routine grafiche potenti e compatte.
· Per quanto riguarda l’efficienza computazionale, aspetto determinante perchè valuta i tempi
effettivi di addestramento, negli esempi appena visti siamo giunti ad un comportamento accettabile
del sistema già con pochissimi passi, il che è stato naturalmente favorito dalla ristrettezza dei
dominii del problema, ovvero quello dello stato iniziale e quello dei disturbi sul sistema.
Spesso, anche nelle applicazioni che coinvolgono più in generale le reti neuali, ciò non accade
o si cercano soluzioni tendenti maggiormente all’ottimo. Diventano così necessari moltissimi
passi di addestramento in più, in questo caso per sottoporre il sistema ad un numero elevato
di ingressi e disturbi sul sistema di test, ed è proprio qui che la velocità computazionale
della versione in C del modello diventa apprezzabile.
· Possiamo ancora osservare che, sopratutto nell’implementazione C, risulta ottimizzabile
l’accesso al file system, cosa che consentirebbe un lieve e ulteriore miglioramento delle
prestazioni.
L’esempio applicativo che abbiamo qui implementato, per le motivazioni appena analizzate,
lascia intravedere enormi vantaggi nell’uso del C, soprattutto per quei problemi di controllo
ottimo basati su reti approssimanti nei quali sono necessari molti passi di addestramento,
mentre porta a considerare l’approccio basato su Matlab più utile per problemi “ristretti”, dove
la facilità d’uso e la semplicità di accesso alle informazioni assumono maggior peso rispetto ai
tempi risolutivi.

Ringraziamenti,
Introduzione,
Capitolo 1,
Capitolo 2,
Capitolo 3,
Capitolo 4,
Bibliografia
 , altrimenti questa condizione non sarebbe
essenziale (contesto deterministico), ma è bene che sia comunque soddisfatta, per essere
in grado di fronteggiare il caso in cui dovessero verificarsi scostamenti imprevisti dalla
traiettoria “deterministica”.
, altrimenti questa condizione non sarebbe
essenziale (contesto deterministico), ma è bene che sia comunque soddisfatta, per essere
in grado di fronteggiare il caso in cui dovessero verificarsi scostamenti imprevisti dalla
traiettoria “deterministica”.
 è il vettore di stato del sistema
dinamico tempo-variante,
è il vettore di stato del sistema
dinamico tempo-variante, 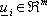 quello dei
controlli. La funzione di costo, non necessariamente quadratica, è invece definita da
quello dei
controlli. La funzione di costo, non necessariamente quadratica, è invece definita da
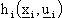 è il costo di transizione
da uno stato al successivo, mentre
è il costo di transizione
da uno stato al successivo, mentre 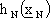 rappresenta il costo sullo stato stato finale, esprimibile in
rappresenta il costo sullo stato stato finale, esprimibile in
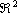 ad esempio quale distanza dall’obiettivo
finale
ad esempio quale distanza dall’obiettivo
finale
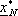 stato finale che si desidera raggiungere.
stato finale che si desidera raggiungere.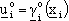 (feedback sullo stato, “anello chiuso”)
con i = 0, 1, ..., N-1, tale da minimizzare il costo J.
(feedback sullo stato, “anello chiuso”)
con i = 0, 1, ..., N-1, tale da minimizzare il costo J.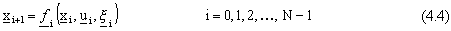

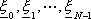 è una sequenza di vettori
aleatori misurabili con densità di probabilità
è una sequenza di vettori
aleatori misurabili con densità di probabilità 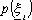 nota, che rappresenta il disturbo sul sistema.
nota, che rappresenta il disturbo sul sistema.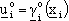 , con i = 0, 1, ..., N-1, tale da
minimizzare il valor medio del costo J.
, con i = 0, 1, ..., N-1, tale da
minimizzare il valor medio del costo J.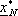 appartiene ad un compatto
appartiene ad un compatto
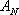 , anziché essere un unico stato finale
desiderato, risolvere il problema con la programmazione dinamica equivale a definire più problemi,
uno per ogni possibile
, anziché essere un unico stato finale
desiderato, risolvere il problema con la programmazione dinamica equivale a definire più problemi,
uno per ogni possibile 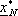 obiettivo. Tutto ciò
si traduce in un’enorme complessità di calcolo, accompagnata da un’ingente richiesta di memoria
per memorizzare gli stati con i rispettivi controlli.
obiettivo. Tutto ciò
si traduce in un’enorme complessità di calcolo, accompagnata da un’ingente richiesta di memoria
per memorizzare gli stati con i rispettivi controlli.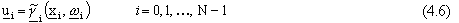
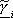 ha la struttura di rete approssimante
(nell’esempio qui trattato una multilayer feed-forward neural network) e
ha la struttura di rete approssimante
(nell’esempio qui trattato una multilayer feed-forward neural network) e
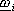 il rispettivo vettore dei parametri liberi
da ottimizzare, ovvero il vettore dei pesi.
il rispettivo vettore dei parametri liberi
da ottimizzare, ovvero il vettore dei pesi.

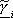 ,
solitamente scelte con la medesima struttura, hanno il compito di generare il controllo
,
solitamente scelte con la medesima struttura, hanno il compito di generare il controllo
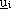 che viene passato al sistema dinamico,
ovvero alla funzione di stato, per generare il nuovo vettore di stato
che viene passato al sistema dinamico,
ovvero alla funzione di stato, per generare il nuovo vettore di stato
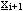 .
.

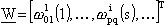 come il vettore di
tutti i pesi delle singole reti, dove
come il vettore di
tutti i pesi delle singole reti, dove 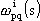 rappresenta il peso del neurone q appartenente al livello s della rete
i sull’uscita p del livello s-1.
rappresenta il peso del neurone q appartenente al livello s della rete
i sull’uscita p del livello s-1.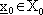 , possiamo modificare il costo nella
seguente maniera:
, possiamo modificare il costo nella
seguente maniera: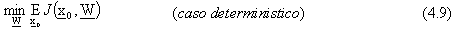
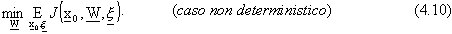
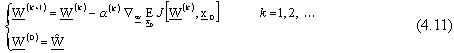
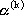 è una funzione che definisce la lunghezza
del passo di discesa, decrescente con k per assicurare la convergenza al punto ottimo
è una funzione che definisce la lunghezza
del passo di discesa, decrescente con k per assicurare la convergenza al punto ottimo
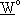 e solitamente espressa come:
e solitamente espressa come:
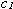 e
e
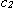 costanti da determinare.
costanti da determinare. ,
si preferisce ricorrere alla tecnica del “gradiente stocastico” e calcolare pertanto
,
si preferisce ricorrere alla tecnica del “gradiente stocastico” e calcolare pertanto
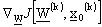 , estraendo ad ogni passo di iterazione
k il vettore
, estraendo ad ogni passo di iterazione
k il vettore 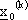 dal dominio compatto
dal dominio compatto
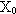 , secondo l’opportuna distribuzione di
probabilità.
, secondo l’opportuna distribuzione di
probabilità.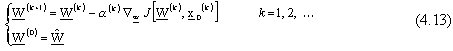
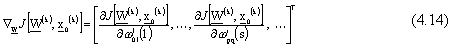


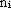 il livello s della rete i
e q = 1, ...,
il livello s della rete i
e q = 1, ..., 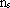 il suo
corrispondente neurone q.
il suo
corrispondente neurone q.
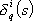 possono essere calcolate
ricorsivamente dal seguente sistema
possono essere calcolate
ricorsivamente dal seguente sistema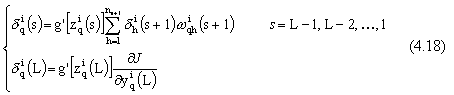
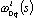 nella (4.17) sono ottenute impostando
il corrispondente ingresso q a 1.
nella (4.17) sono ottenute impostando
il corrispondente ingresso q a 1.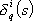 , è necessario determinare le componenti
q del vettore
, è necessario determinare le componenti
q del vettore 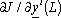 , ovvero le derivate
parziali di J rispetto all’uscita q dell’ultimo livello della rete i,
attraverso
, ovvero le derivate
parziali di J rispetto all’uscita q dell’ultimo livello della rete i,
attraverso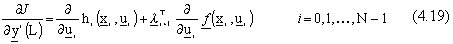
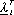 sono ottenute anch’esse
ricorsivamente dal sistema:
sono ottenute anch’esse
ricorsivamente dal sistema: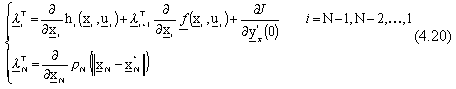

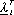 è riconducibile alla teoria del controllo ottimo in N-stadi, con l’aggiuna di
è riconducibile alla teoria del controllo ottimo in N-stadi, con l’aggiuna di
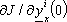 che permette di cosiderare l’introduzione
delle reti neurali.
che permette di cosiderare l’introduzione
delle reti neurali.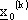 da
da
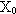 , sono generate la sequenza dei controlli e
la traiettoria dello stato, che dipendono da
, sono generate la sequenza dei controlli e
la traiettoria dello stato, che dipendono da 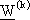
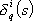 e
e
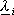 a ritroso, viene determinato il gradiente
a ritroso, viene determinato il gradiente
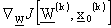 che consente di eseguire un passo di
discesa e di trovare così
che consente di eseguire un passo di
discesa e di trovare così 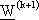
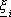 , il problema di
programmazione non lineare si trasforma nel determinare la sequenza delle leggi o funzioni
ottime decisionali
, il problema di
programmazione non lineare si trasforma nel determinare la sequenza delle leggi o funzioni
ottime decisionali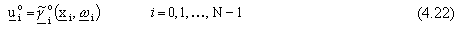
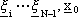 , ovvero:
, ovvero:

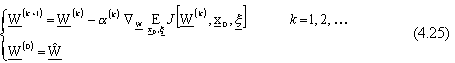
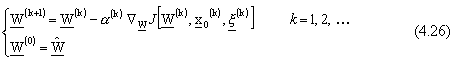
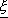 dei disturbi aleatori sul sistema, si
ottiene un algoritmo di apprendimento analogo al precedente, con la sola differenza che nella
fase forward devono essere estratte anche le componenti
dei disturbi aleatori sul sistema, si
ottiene un algoritmo di apprendimento analogo al precedente, con la sola differenza che nella
fase forward devono essere estratte anche le componenti
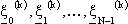 .
.
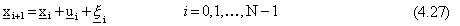
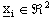 è il vettore di stato con
è il vettore di stato con
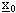 appartenente al dominio del problema
(la dimensione è 2 solo per motivi di rappresentazione grafica),
appartenente al dominio del problema
(la dimensione è 2 solo per motivi di rappresentazione grafica),
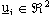 il controllo generato dalla rete
i-esima a 2 strati del trenino, mentre
il controllo generato dalla rete
i-esima a 2 strati del trenino, mentre
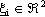 rappresenta il disturbo che agisce sul
sistema, estratto casualmente secondo una distribuzione uniforme specificata di volta in volta
(così come
rappresenta il disturbo che agisce sul
sistema, estratto casualmente secondo una distribuzione uniforme specificata di volta in volta
(così come 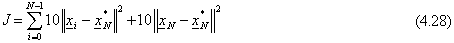
 , si può inizialmente addestrare il
“treno” per condurre il sistema da un solo stato inziale
, si può inizialmente addestrare il
“treno” per condurre il sistema da un solo stato inziale


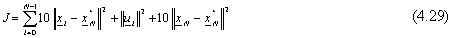


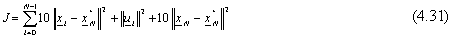
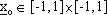 , N = 1 e sul sistema non
agisce alcun disturbo, già con 500 passi di addestramento si ottiene un buon risultato,
, N = 1 e sul sistema non
agisce alcun disturbo, già con 500 passi di addestramento si ottiene un buon risultato,
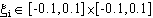 ,
la traiettoria può “deviare” dall’obiettivo, come mostrato in figura 4-9.
,
la traiettoria può “deviare” dall’obiettivo, come mostrato in figura 4-9.
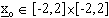 e soprattutto
e soprattutto
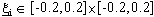 , lo stato finale desiderato è raggiunto
con maggiore difficoltà (figura 4-10).
, lo stato finale desiderato è raggiunto
con maggiore difficoltà (figura 4-10).
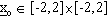 e con 50 neuroni al primo livello di ogni
rete, otteniamo il comportamento di figura 4-11.
e con 50 neuroni al primo livello di ogni
rete, otteniamo il comportamento di figura 4-11.
