CAPITOLO 1
Reti Approssimanti
1.1 Introduzione
Gli approssimatori non lineari, di cui forniremo nel seguito alcune basi teoriche, possono
essere utilizzati per approssimare funzioni tipiche della teoria del controllo, quali funzioni
di costo o di controllo ottimo.
In questo capitolo saranno analizzati vari schemi di approssimazione, introducendo criteri di
confronto basati sulla loro complessità (in termini computazionali e di ingombro di memoria),
che permetteranno di constatare la bontà degli schemi non lineari rispetto a quelli lineari.
Nel seguito, fra le varie reti approssimanti, descriveremo in dettaglio due particolari classi,
le Multilayer Feed-forward Neural Networks e le Radial Basis Functions,
distinguibili per le caratteristiche delle unità e/o per il modo in cui queste sono connesse
tra loro. Le prime verranno poi scelte per la nostra implementazione al calcolatore.
1.2 Modello delle reti approssimanti
Nella ricerca di metodi approssimati capaci di risolvere problemi di controllo ottimo, come ad
esempio il problema del controllo ottimo a N stadi, un possibile approccio consiste nel sostituire
al problema originario problemi approssimati di più agevole definizione e risoluzione.
Per formalizzare questi sotto-problemi usiamo funzioni approssimanti dotate di una struttura
fissata, dove occorre determinare il valore di un dato numero di parametri attraverso metodi
di programmazione non lineare, al fine di minimizzare un costo che quantifica, in un qualche
modo, la differenza tra la funzione e la sua realizzazione.
Poniamo quindi:

con 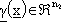 funzione da approssimare,
funzione da approssimare,
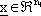 vettore di stato,
vettore di stato,
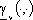 funzione di struttura fissata,
funzione di struttura fissata,
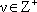 e
e
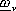 vettore dei parametri di dimensione
finita da determinare, ed assegnamo alla j-esima componente della funzione
vettore dei parametri di dimensione
finita da determinare, ed assegnamo alla j-esima componente della funzione
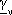 la struttura:
la struttura:

dove 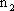 è la dimensione della funzione da
approssimare,
è la dimensione della funzione da
approssimare, 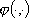 una data funzione di base,
mentre i
una data funzione di base,
mentre i 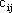 e le componenti di
e le componenti di
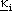 sono i parametri da determinare.
sono i parametri da determinare.
Sia ora 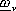 il vettore così strutturato:
il vettore così strutturato:
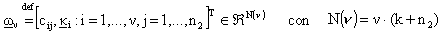
Definendo poi 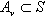 l’insieme parametrizzato
di tutte le funzioni, le cui componenti hanno la forma data in (1.2), si ottiene:
l’insieme parametrizzato
di tutte le funzioni, le cui componenti hanno la forma data in (1.2), si ottiene:
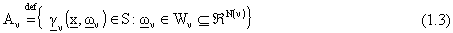
dove 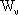 è l’insieme dei valori ammissibili
per i parametri, secondo i limiti stabiliti dall’insieme S. Si può allora affermare che
la sequenza degli insiemi
è l’insieme dei valori ammissibili
per i parametri, secondo i limiti stabiliti dall’insieme S. Si può allora affermare che
la sequenza degli insiemi 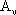 al variare del
parametro
al variare del
parametro  ha una struttura annidata di
questo tipo:
ha una struttura annidata di
questo tipo:

Si assuma che lo spazio all’interno del quale cerchiamo le funzioni da approssimare sia dotato
di norma  . Inoltre le funzioni
. Inoltre le funzioni
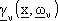 siano tali che l’insieme
siano tali che l’insieme
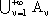 sia denso in S.
sia denso in S.
Sotto queste ipotesi, definiamo allora reti approssimanti le funzioni
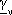 le cui componenti hanno la forma in (1.2)
e che sono dotate della proprietà di densità. La complessità in termini computazionali e di
ingombro di memoria di una rete così definita è riconducibile alla dimensione del vettore dei
parametri da ottimizzare
le cui componenti hanno la forma in (1.2)
e che sono dotate della proprietà di densità. La complessità in termini computazionali e di
ingombro di memoria di una rete così definita è riconducibile alla dimensione del vettore dei
parametri da ottimizzare 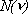 .
.
Nel caso in cui le funzioni da approssimare siano continue su un insieme compatto K,
la proprietà di densità ci porta a definire formalmente una “rete approssimante” nel modo
seguente:
Definizione 1 Una rete approssimante nella forma (1.2) si dice di
Weierstrass se, data una funzione continua 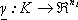 ,
,
per ogni 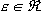 ,
con
,
con 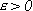 , esistono vettori di parametri
, esistono vettori di parametri
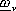 tali che:
tali che:
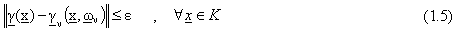
La disuguaglianza (1.5) assicura l’esistenza, per ogni funzione continua, di una rete
approssimante (1.2), dalla quale si ottiene un’approssimazione, a meno dell’errore
 , della funzione stessa.
, della funzione stessa.
L’impiego pratico di questi strumenti, talvolta anche definiti “approssimatori universali”,
richiede qualche ulteriore precisazione in merito alle tecniche di costruzione delle funzioni
base parametrizzate 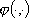 .
.
La procedura più diffusa consiste nel derivare le funzioni base da una singola funzione
monodimensionale o da una famiglia di funzioni monodimensionali. Fra le tecniche più usate,
ricordiamo:
1) Tensor product construction:

dove 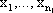 sono le
componenti del vettore
sono le
componenti del vettore 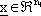 ,
,
con 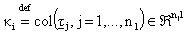 .
.
È usata nella costruzione di funzioni base polinomiali e splines per l’approssimazione
multidimensionale basata su griglie.
2) Ridge construction:
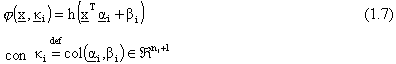
Ad esempio, nel caso delle reti neurali Multilayer Feedforward con uno strato nascosto,
la j-esima componente della rete è:

dove 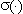 è la funzione di attivazione,
solitamente sigmoidale.
è la funzione di attivazione,
solitamente sigmoidale.
3) Radial construction:
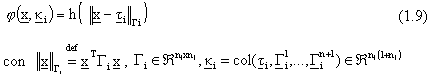
dove 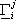 rappresenta
la j-esima colonna della matrice
rappresenta
la j-esima colonna della matrice 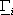 .
.
Ad esempio, nelle Radial Basis Function, la j-esima componente è scrivibile
come segue:

Le reti approssimanti così ottenute godono della proprietà di densità nei due spazi che abbiamo
definito, il che ne giustifica l’appartenenza alla classe delle reti approssimanti di Weierstrass.
L’approssimazione multivariabile mediante funzione base costruite con la “tensor product”, basata
su griglie, è usata raramente in problemi con una dimensione non modesta. Invece, la ridge
e la radial construction pongono meno limiti alle dimensioni del problema.
1.3 “Rate di approssimazione”
Nel caso in cui soddisfino la proprietà di densità, abbiamo visto che le reti approssimanti
possono essere usate come “approssimatori universali”. Ma ciò vale anche per i più “classici”
approssimatori lineari, definibili come:
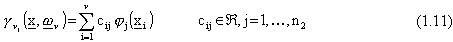
dove le 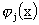 sono funzioni base linearmente
indipendenti.
sono funzioni base linearmente
indipendenti.
La caratteristica che invece fa la differenza e che rende interessante l’uso delle reti, rispetto
all’altra classe di approssimatori, è il comportamento del “rate dell’approssimazione”, ovvero la
relazione fra l’accuratezza dell’approssimazione ricavabile da un dato schema approssimante e la
complessità di tale schema in termini computazionali e di ingombro di memoria, quantificabile
considerando la dimensione del vettore dei parametri.
Una relazione di questo tipo “misura” quanto rapidamente l’errore di approssimazione vada a zero
al tendere all’infinito della dimensione del vettore dei parametri. Un esempio sono le reti
neurali Feedforward, impiegate per approssimare, con un numero in alcuni casi molto limitato di
parametri, funzioni di decine di variabili. Prima di parlare del “rate” è utile introdurre alcune
definizioni che permettono di effettuare ora in modo efficiente confronti fra i vari schemi di
approssimazione.
Considerando un insieme S, sottoinsieme di uno spazio normato H i cui elementi
siano funzioni scalari 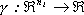 , definiamo la
deviazione di S dall’insieme A come:
, definiamo la
deviazione di S dall’insieme A come:

dove  è la norma dello spazio H.
Quindi
è la norma dello spazio H.
Quindi 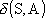 misura l’errore di approssimazione
di funzioni appartenenti all’insieme S mediante funzioni appartenenti ad A,
valutando sempre la funzione peggio approssimata.
misura l’errore di approssimazione
di funzioni appartenenti all’insieme S mediante funzioni appartenenti ad A,
valutando sempre la funzione peggio approssimata.
Sia dato ora un insieme di funzioni parametrizzate 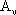 ,
dal quale trarre le funzioni approssimanti. Quando lo schema di approssimazione
,
dal quale trarre le funzioni approssimanti. Quando lo schema di approssimazione
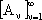 è lineare e l’insieme S delle
soluzioni ammissibili è anch’esso uno spazio lineare, allora ognuno degli insiemi
è lineare e l’insieme S delle
soluzioni ammissibili è anch’esso uno spazio lineare, allora ognuno degli insiemi
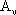 è un sottoinsieme parametrizzato di H.
è un sottoinsieme parametrizzato di H.
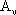 è ottenuto selezionando dagli elementi di
un sottospazio
è ottenuto selezionando dagli elementi di
un sottospazio 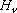
 -dimensionale quelli che soddisfano i vincoli
che definiscono l’insieme S delle soluzioni ammissibili. In questo caso si ha:
-dimensionale quelli che soddisfano i vincoli
che definiscono l’insieme S delle soluzioni ammissibili. In questo caso si ha:

poiché 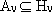 .
.
Per ottenere un limite inferiore per il rate del miglior schema di approssimazione lineare
nell’approssimazione di funzioni appartenenti all’insieme S, possiamo allora definire
la quantità:

in cui l’inf viene eseguito rispetto a tutti i sottoinsiemi
 -dimensionali
-dimensionali
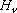 di H, cioè su tutti gli schemi di
approssimazione lineari. Nel caso non lineare è possibile confrontare i “rate di approssimazione”
di due diversi schemi di approssimazione non lineari
di H, cioè su tutti gli schemi di
approssimazione lineari. Nel caso non lineare è possibile confrontare i “rate di approssimazione”
di due diversi schemi di approssimazione non lineari
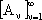 e
e
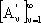 , in termini delle due deviazioni
, in termini delle due deviazioni
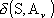 e
e
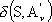 .
.
Se invece si desidera confrontare uno schema di approssimazione non lineare con il migliore schema
lineare, allora si fa riferimento a 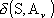 e
e
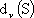 . In generale l’errore espresso da
. In generale l’errore espresso da
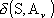 e da
e da
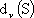 , per una fissata complessità nu,
cresce con la dimensione n, e perciò l’obiettivo è quello di evitare schemi nei quali
tale crescita sia troppo rapida, cioè richieda, per grandi valori di n, un numero
eccessivamente elevato
, per una fissata complessità nu,
cresce con la dimensione n, e perciò l’obiettivo è quello di evitare schemi nei quali
tale crescita sia troppo rapida, cioè richieda, per grandi valori di n, un numero
eccessivamente elevato  di funzioni base.
di funzioni base.
Alla luce di quanto detto, il “rate di approssimazione”, utile per un paragone fra differenti
schemi di approssimazione, può essere definito anche considerando il comportamento dell’errore nel
caso peggiore, ovvero per la funzione peggio approssimata, in dipendenza da
 e n.
e n.
Dal momento che espressioni esatte per questa dipendenza sono ottenibili soltanto in casi
particolari, il confronto può essere effettuato sulla base di limiti superiori noti per questo
errore.
Si dice pertanto indipendente dalla dimensione un rate di approssimazione per il quale
esiste un limite superiore 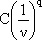 con
con
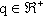 e C costante indipendente da
e C costante indipendente da
 e n. Quando invece il miglior
limite superiore ottenibile ha una forma del tipo
e n. Quando invece il miglior
limite superiore ottenibile ha una forma del tipo 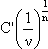 ,
dove C’ è una costante sempre indipendente da
,
dove C’ è una costante sempre indipendente da
 e n, allora per commettere nel
caso peggiore un errore
e n, allora per commettere nel
caso peggiore un errore  , possono essere
richieste funzioni approssimanti di complessità
, possono essere
richieste funzioni approssimanti di complessità  .
.
Una tale dipendenza esponenziale dalla dimensione n dà origine alla maledizione della
dimensionalità e uno schema di approssimazione affetto da questo problema è inapplicabile su
grandi dimensioni. Questa sostanziale differenza di comportamento distingue schemi ammissibili
da schemi non ammissibili e può essere quindi impiegata come criterio per scegliere un
tipo di rete approssimante piuttosto che un altro per la soluzione di problemi di ottimizzazione,
sebbene in generale questa distinzione così netta non sia semplice da effettuare.
Tipicamente C e C’ sono costanti rispetto a
 , ma dipendono invece dalla dimensione
n. Quando tali valori mostrano una crescita rapida con n, il limite superiore
perde sempre più significato al crescere della dimensione.
, ma dipendono invece dalla dimensione
n. Quando tali valori mostrano una crescita rapida con n, il limite superiore
perde sempre più significato al crescere della dimensione.
Data ora la seguente classe di funzioni da approssimare
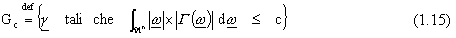
dove:
· 
· 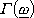 è la trasformata di fourier di
è la trasformata di fourier di
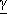
· c è uno scalare positivo finito
si dimostra [1] che, utilizzando lo schema approssimante
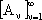 rappresentato da reti neurali feedforward
sigmoidali su funzioni da approssimare appartenenti a questo insieme si ottiene:
rappresentato da reti neurali feedforward
sigmoidali su funzioni da approssimare appartenenti a questo insieme si ottiene:
Teorema 1 (Barron 1993) :
In 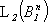 , dove
, dove
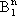 è la sfera di raggio unitario in
è la sfera di raggio unitario in
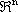 ,
,

essendo 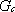 l’insieme definito in (1.15)
e C = 2c.
l’insieme definito in (1.15)
e C = 2c.
Da ciò segue un importante risultato: il numero di parametri richiesto da una rete neurale
feedforward sigmoidale per ottenere in 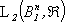 un errore di approssimazione dell’ordine di
un errore di approssimazione dell’ordine di 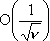 è
è 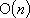 , ovvero cresce soltanto linearmente con
la dimensione n del vettore di stato.
, ovvero cresce soltanto linearmente con
la dimensione n del vettore di stato.
Nello stesso articolo, si dimostra che nell’insieme
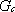 gli schemi lineari possono comportarsi
in modo peggiore, fino a richiedere una crescita esponenziali di
gli schemi lineari possono comportarsi
in modo peggiore, fino a richiedere una crescita esponenziali di
 con n (maledizione della
dimensionalità) per mantenere contenuto l’errore di approssimazione.
con n (maledizione della
dimensionalità) per mantenere contenuto l’errore di approssimazione.
Gli importanti risultati ottenuti in [1], sebbene rappresentino comunque un primo tentativo per il
confronto di schemi lineari e non lineari nell’approssimazione di una vasta classe di funzioni,
non bastano però a spiegare completamente il migliore comportamento delle reti approssimanti
neurali in sistemi di dimensione elevata, dal momento che c potrebbe anche crescere
esponenzialmente con n.
Tuttavia, recenti direzioni di studio (per esempio, si vedano [2], [3] e [4]) sembrano confermare
la bontà degli approssimatori non lineari rispetto a quelli lineari, portando perciò a concludere
che, dato uno schema non lineare rappresentato da una rete approssimante
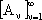 , sotto opportune ipotesi esiste un insieme
di funzioni B, dipendente dallo schema
, sotto opportune ipotesi esiste un insieme
di funzioni B, dipendente dallo schema
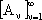 , tale che:
, tale che:
1) 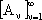 ottiene per le funzioni appartenenti
a B un rate indipendente dalla dimensione
ottiene per le funzioni appartenenti
a B un rate indipendente dalla dimensione
2) il miglior schema lineare di approssimazione ha, per le funzioni appartenenti allo stesso
insieme, un rate limitato inferiormente da un valore che può dipendere esponenzialmente dalla
dimensione.
Quindi, per questo insieme di funzioni si ha:

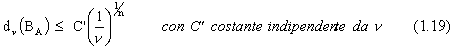
Se C’ non tende a zero con la dimensione n, quando per esempio non dipende da
essa, allora per le funzioni appartenenti all’insieme B qualsiasi schema di
approssimazione lineare è affetto dalla maledizione della dimensionalità, diversamente
dall’approssimazione con “rate” indipendente dalla dimensione ottenuta dallo schema
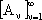 per lo stessa classe di funzioni.
per lo stessa classe di funzioni.
Una seconda direzione di ricerca, sempre a riguardo di un confronto generale fra rate di
approssimazione, è incentrata su un risultato relativo agli approssimatori lineari e non lineari
parametrizzati (con dipendenza continua dei parametri dalla funzione da approssimare), noto come
“Jackson rate”.
Si dimostra infatti che, se la funzione da approssimare è derivabile con derivate continue fino
al grado s ed ha n variabili, non è possibile ottenere un’approssimazione con
accuratezza migliore di:

detto Jackson rate, con p numero dei parametri. In questo modo, quando il
coefficiente di regolarità s della funzione viene fatto crescere con la dimensione
n, è possibile ottenere una stima non esponenziale del limite superiore del numero
di parametri necessari.
Sebbene il risultato della (1.20) rappresenti un limite inferiore stretto per gli schemi di
approssimazione lineari, può non esserlo per quelli non lineari. Infatti, il Jackson rate
viene ricavato per gli approssimatori non lineari parametrizzati con dipendenza continua dei
parametri ottimi dalla funzione da approssimare, caratteristica che si rivela non necessaria
per la costruzione di uno schema non lineare, dove potrebbe non essere valido un limite
inferiore come quello stabilito in (1.20) e il suo rate allora risultare migliore.
Riassumendo, in spazi caratterizzati da particolari requisiti di regolarità delle funzioni e
delle loro derivate parziali, gli approssimatori non lineari sono in grado di raggiungere
gli stessi rate di convergenza di quelli lineari, nel caso in cui si restringa la trattazione a
considerare solo quegli schemi i cui parametri presentano una dipendenza continua dalla
funzione da approssimare.
Quando invece si considerano i casi con dipendenza non continua, è possibile che fra questi si
possano ottenere tassi di convergenza anche migliori. Al contrario esistono insiemi di funzioni
nei quali gli schemi di approssimazione lineari presentano il problema della maledizione della
dimensionalità, laddove esiste almeno uno schema non lineare che permette di ottenere un tasso
di convergenza indipendente dalla dimensione.
L’utilizzo di schemi non lineari per la soluzione approssimata di problemi di controllo ottimo
si rivela quindi essere una scelta valida sostanzialmente per due motivi:
1°) da un punto di vista teorico offre la possibilità di ottenere rate di convergenza
indipendenti dalla dimensione, non solo per gli insiemi di funzioni in cui anche gli
approssimatori lineari possono riuscirvi, ma anche in quelli dove l’uso di schemi lineari
soffre della maledizione della dimensionalità
2°) da un punto di vista pratico offre buone prestazioni, sia in riferimento all’occupazione di
memoria sia per quanto riguarda la complessità computazionale, a fronte di una accuratezza
soddisfacente delle approssimazioni ottenute confrontate con quelle che si ottengono per altre vie.
1.4 “Addestramento” reti approssimanti
La fase di addestramento prevede l’ottimizzazione dei parametri liberi (detti comunemente
pesi) della rete, che avviene risolvendo problemi di programmazione non lineare.
Se ci riferiamo all’uso delle reti approssimanti per approssimazioni di funzioni, durante
la fase di addestramento un insieme (set) di L punti, nei quali si conosce il valore
della funzione da approssimare, viene presentato in ingresso alla rete. Lo scopo è allora
minimizzare una funzione di costo J che penalizza, ad esempio, l’errore quadratico
medio fra l’uscita della rete e il valore vero della funzione valutata nei punti di
addestramento.
La funzione di costo J è perciò esprimibile come
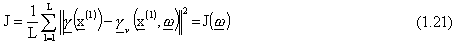
dove:
· 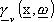 è l’uscita della rete la cui
j-esima componente è data nell’equazione (1.8)
è l’uscita della rete la cui
j-esima componente è data nell’equazione (1.8)
· L è la dimensione del “training set”
· 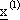 è l’l-esimo punto di
addestramento
è l’l-esimo punto di
addestramento
· 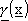 è la funzione da approssimare.
è la funzione da approssimare.
Il problema di programmazione non linerare diventa quindi:

A questo punto è possibile scegliere un algoritmo di programmazione non lineare, per esempio
il metodo del gradiente, quale tecnica per risolvere il problema di minimizzazione e portare
a buon fine il processo di addestramento.
Nell’addestramento delle reti neurali, la procedura del gradiente è nota come “back propagation”,
come vedremo nel capitolo 2.
1.5 Reti neurali Multilayer Feed-Forward
Le Reti Neurali Multilayer Feedforward sono strutture multistrato che sottopongono una
combinazione lineare delle componenti del vettore di input all’ingresso di blocchi non lineari
di “attivazione”, le uscite dei quali vengono a loro volta poste all’ingresso di altre non
linearità, fino allo strato di uscita.
Le reti di tipo feedforward con un singolo strato nascosto sono esempi di reti approssimanti,
le cui funzioni base sono costruite mediante la “ridge construction”. Ricordiamo che la struttura
della j-esima componente di una rete multipercettrone con uno strato nascosto può essere
così definita:

Nel caso generale di un numero L di strati, la struttura globale, data dalla
interconnessione di più unità di processing, assume la forma qui mostrata nella figura 1-1:
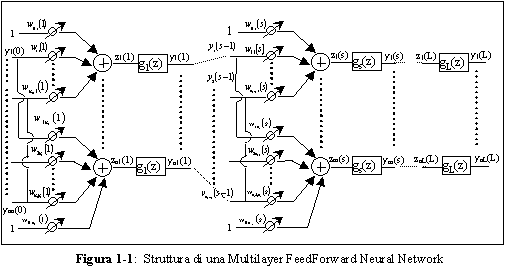
dove:
· 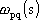 è il peso relativo alla p-esima
componente del vettore in ingresso al neurone q-esimo dello strato s
è il peso relativo alla p-esima
componente del vettore in ingresso al neurone q-esimo dello strato s
· 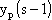 è l’uscita del p-esimo neurone
dello strato s-1
è l’uscita del p-esimo neurone
dello strato s-1
· 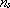 è la dimensione del vettore di ingresso
allo strato s o equivalentemente quello dei suoi neuroni
è la dimensione del vettore di ingresso
allo strato s o equivalentemente quello dei suoi neuroni
· 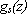 è la funzione di attivazione, che
definisce l’output della singola unità di processing appartenente allo strato s.
è la funzione di attivazione, che
definisce l’output della singola unità di processing appartenente allo strato s.
Le strutture più usate come funzioni di attivazione, nonché quelle per cui valgono tutti i
risultati dati nel seguito, sono funzioni sigmoidali, ossia funzioni continue e
limitate sull’asse reale, tali che:


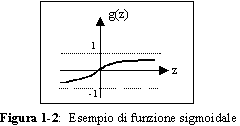
Un tipico esempio di funzione sigmoidale è il seguente:

il cui grafico è mostrato in figura 1-2.
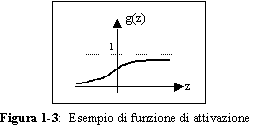
Fra le altre funzioni di attivazione frequentemente utilizzate, ricordiamo:

rappresentata in figura 1-3.
1.6 Radial Basis Functions
Le Radial Basis Functions (RBF) consentono la risoluzione di problemi di interpolazione
multivariabile: il loro utilizzo all’interno della struttura di una rete neurale permette di
ottenere superfici nello spazio multidimensionale che forniscono un “fitting” ottimale in senso
statistico per i dati in ingresso.
La struttura della j-esima componente di una rete approssimante di questo tipo, le cui
funzioni base sono costruite mediante la “radial construction”, è la seguente:

Le reti approssimanti RBF richiedono un numero di neuroni nello strato nascosto tipicamente
molto maggiore rispetto a quello delle reti feed-forward, a fronte però di un tempo di
addestramento notevolmente più ridotto. Inoltre forniscono risultati migliori quando si hanno
a disposizione un numero elevato di punti di osservazione (cioè quando si conoscono valori veri
o approssimati della funzione in un elevato numero di punti).
La loro architettura più comune può essere così schematizzata:
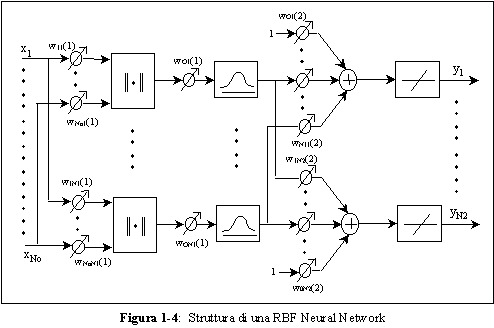
La rete è composta dunque da due strati, uno nascosto e uno di uscita. In ingresso allo strato
nascosto viene presentata la norma del vettore di ingresso a cui si sottrae il vettore “centro”
della gaussiana.
I neuroni di questo strato sono caratterizzati da una funzione di attivazione gaussiana del tipo:

con:
· 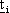 centro della gaussiana
centro della gaussiana
· 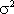 varianza.
varianza.
La combinazione lineare pesata delle uscite dello strato nascosto viene portata in ingresso ad
uno strato lineare di uscita.
A questo punto occorre centrare nello spazio multidimensionale le RBF approssimanti sui punti di
osservazione (mediante lo strato nascosto), per poi modulare, tramite lo strato lineare, sui
valori della funzione in quei punti.
Alla fine la rete ottimizzata avrà un numero di neuroni dello strato nascosto (quello con funzioni
di attivazione gaussiane) circa uguale al numero di punti di osservazione.
La rete appena descritta viene addestrata con un algoritmo di tipo incrementale, dove
inizialmente lo strato nascosto è privo di neuroni, quindi ad ogni passo dell’algoritmo la rete
viene simulata e si aggiunge un’unità neurale con funzione di attivazione gaussiana, i cui pesi
vengono determinati sulla base del valore del vettore di ingresso per il quale si è riscontrato
un errore maggiore (dell’output della precedente simulazione rispetto al valore vero).
I pesi dello strato lineare vengono poi ottimizzati al fine di minimizzare l’errore. L’algoritmo
prosegue fino al raggiungimento dell’errore quadratico medio che si vuole ottenere dalla rete.

Ringraziamenti,
Introduzione,
Capitolo 1,
Capitolo 2,
Capitolo 3,
Capitolo 4,
Bibliografia

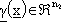 funzione da approssimare,
funzione da approssimare,
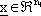 vettore di stato,
vettore di stato,
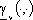 funzione di struttura fissata,
funzione di struttura fissata,
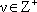 e
e
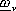 vettore dei parametri di dimensione
finita da determinare, ed assegnamo alla j-esima componente della funzione
vettore dei parametri di dimensione
finita da determinare, ed assegnamo alla j-esima componente della funzione
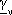 la struttura:
la struttura:
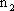 è la dimensione della funzione da
approssimare,
è la dimensione della funzione da
approssimare, 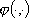 una data funzione di base,
mentre i
una data funzione di base,
mentre i 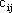 e le componenti di
e le componenti di
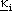 sono i parametri da determinare.
sono i parametri da determinare.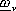 il vettore così strutturato:
il vettore così strutturato: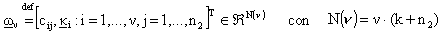
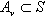 l’insieme parametrizzato
di tutte le funzioni, le cui componenti hanno la forma data in (1.2), si ottiene:
l’insieme parametrizzato
di tutte le funzioni, le cui componenti hanno la forma data in (1.2), si ottiene: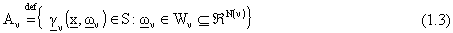
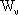 è l’insieme dei valori ammissibili
per i parametri, secondo i limiti stabiliti dall’insieme S. Si può allora affermare che
la sequenza degli insiemi
è l’insieme dei valori ammissibili
per i parametri, secondo i limiti stabiliti dall’insieme S. Si può allora affermare che
la sequenza degli insiemi 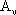 al variare del
parametro
al variare del
parametro  ha una struttura annidata di
questo tipo:
ha una struttura annidata di
questo tipo:
 . Inoltre le funzioni
. Inoltre le funzioni
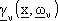 siano tali che l’insieme
siano tali che l’insieme
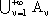 sia denso in S.
sia denso in S.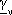 le cui componenti hanno la forma in (1.2)
e che sono dotate della proprietà di densità. La complessità in termini computazionali e di
ingombro di memoria di una rete così definita è riconducibile alla dimensione del vettore dei
parametri da ottimizzare
le cui componenti hanno la forma in (1.2)
e che sono dotate della proprietà di densità. La complessità in termini computazionali e di
ingombro di memoria di una rete così definita è riconducibile alla dimensione del vettore dei
parametri da ottimizzare 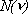 .
.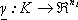 ,
,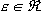 ,
con
,
con 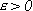 , esistono vettori di parametri
, esistono vettori di parametri
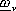 tali che:
tali che: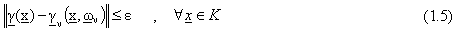
 , della funzione stessa.
, della funzione stessa.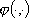 .
.
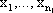 sono le
componenti del vettore
sono le
componenti del vettore 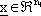 ,
,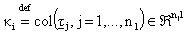 .
.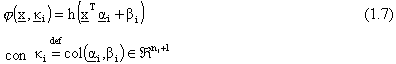

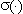 è la funzione di attivazione,
solitamente sigmoidale.
è la funzione di attivazione,
solitamente sigmoidale.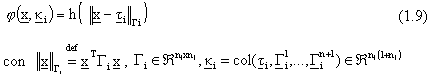
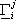 rappresenta
la j-esima colonna della matrice
rappresenta
la j-esima colonna della matrice  .
.
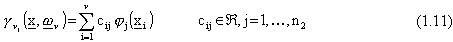
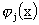 sono funzioni base linearmente
indipendenti.
sono funzioni base linearmente
indipendenti.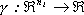 , definiamo la
deviazione di S dall’insieme A come:
, definiamo la
deviazione di S dall’insieme A come:
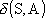 misura l’errore di approssimazione
di funzioni appartenenti all’insieme S mediante funzioni appartenenti ad A,
valutando sempre la funzione peggio approssimata.
misura l’errore di approssimazione
di funzioni appartenenti all’insieme S mediante funzioni appartenenti ad A,
valutando sempre la funzione peggio approssimata.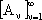 è lineare e l’insieme S delle
soluzioni ammissibili è anch’esso uno spazio lineare, allora ognuno degli insiemi
è lineare e l’insieme S delle
soluzioni ammissibili è anch’esso uno spazio lineare, allora ognuno degli insiemi
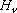

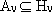 .
.
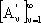 , in termini delle due deviazioni
, in termini delle due deviazioni
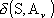 e
e
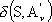 .
.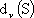 . In generale l’errore espresso da
. In generale l’errore espresso da
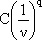 con
con
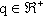 e C costante indipendente da
e C costante indipendente da
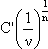 ,
dove C’ è una costante sempre indipendente da
,
dove C’ è una costante sempre indipendente da
 .
.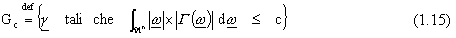

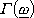 è la trasformata di fourier di
è la trasformata di fourier di
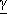
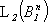 , dove
, dove
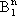 è la sfera di raggio unitario in
è la sfera di raggio unitario in
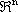 ,
,
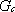 l’insieme definito in (1.15)
e C = 2c.
l’insieme definito in (1.15)
e C = 2c.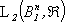 un errore di approssimazione dell’ordine di
un errore di approssimazione dell’ordine di 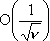 è
è 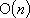 , ovvero cresce soltanto linearmente con
la dimensione n del vettore di stato.
, ovvero cresce soltanto linearmente con
la dimensione n del vettore di stato.
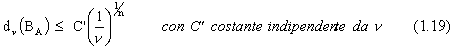

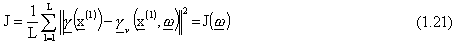
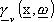 è l’uscita della rete la cui
j-esima componente è data nell’equazione (1.8)
è l’uscita della rete la cui
j-esima componente è data nell’equazione (1.8)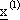 è l’l-esimo punto di
addestramento
è l’l-esimo punto di
addestramento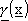 è la funzione da approssimare.
è la funzione da approssimare.


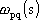 è il peso relativo alla p-esima
componente del vettore in ingresso al neurone q-esimo dello strato s
è il peso relativo alla p-esima
componente del vettore in ingresso al neurone q-esimo dello strato s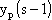 è l’uscita del p-esimo neurone
dello strato s-1
è l’uscita del p-esimo neurone
dello strato s-1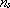 è la dimensione del vettore di ingresso
allo strato s o equivalentemente quello dei suoi neuroni
è la dimensione del vettore di ingresso
allo strato s o equivalentemente quello dei suoi neuroni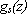 è la funzione di attivazione, che
definisce l’output della singola unità di processing appartenente allo strato s.
è la funzione di attivazione, che
definisce l’output della singola unità di processing appartenente allo strato s.








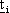 centro della gaussiana
centro della gaussiana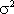 varianza.
varianza.