CAPITOLO 2
Addestramento Reti Neurali
2.1 Introduzione
Nel capitolo precedente abbiamo visto come l’addestramento di una rete approssimante preveda
l’ottimizzazione del vettore dei pesi, finalizzata a determinare quella configurazione ottima
che, minimizzando una certa funzione di costo, porta la rete ad esibire un ben determinato
“comportamento”.
Dal momento che questo processo può essere espresso anche in termini di un problema di
programmazione non lineare, compito dei prossimi paragrafi sarà dunque inizialmente quello di
fornire una panoramica sulle più diffuse tecniche di programmazione non lineare, classificate
a seconda del tipo di informazioni a disposizione sulla funzione da minimizzare, per poi
dedurne i motivi che hanno portato il metodo del gradiente, da cui deriva direttamente la
back-propagation, ad essere il più usato algoritmo per l’addestramento delle reti neurali,
che sono il tipo di rete approssimante che esamineremo più in dettaglio.
2.2 Metodi “diretti”
Con metodi diretti intendiamo quelle tecniche capaci di risolvere un problema di
programmazione non lineare attraverso una “esplorazione” nello spazio degli stati, non avendo
a disposizione alcun tipo di informazione sulla funzione da minimizzare, quale ad esempio il
gradiente o l’hessiana.
Sia dato, ad esempio, il generico problema di programmazione non lineare così formulato:

con n dimensione del vettore di stato, dove si vuole determinare la soluzione ottima
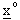 capace di minimizzare la funzione data.
capace di minimizzare la funzione data.
Il più semplice approccio al problema è valutare la funzione in punti diversi e scegliere, di
volta in volta, il miglior candidato al punto di minimo.
Se 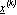 è il punto di minimo al k-esimo
tentativo e
è il punto di minimo al k-esimo
tentativo e 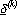 lo spostamento estratto
casualmente che porta in
lo spostamento estratto
casualmente che porta in 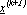 , l’algoritmo può
essere così schematizzato:
, l’algoritmo può
essere così schematizzato:
(a) 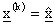
(b) 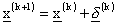
(c) 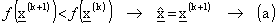 , altrimenti (b) con una nuova
estrazione dello spostamento
, altrimenti (b) con una nuova
estrazione dello spostamento 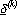 .
.
Un metodo leggermente più evoluto e meglio formalizzato è l’algoritmo di Hooke e Jeeves
che necessita però delle seguenti variabili:
· passo dell’esplorazione locale 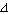
· passo dell’accelearazione 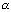
· intervallo di confidenza  .
.
Riferendoci per comodità al caso di figura 2-1 con n = 2, l’algoritimo esegue una
“fase di esplorazione” fra gli 8 punti limitrofi a
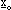 che formano un quadrato di lato
che formano un quadrato di lato
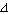 intorno ad esso, fino a quando non trova
il punto
intorno ad esso, fino a quando non trova
il punto 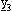 in cui
in cui
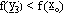 : termina così la prima fase.
: termina così la prima fase.
A questo punto inizia la “fase di accelerazione” in cui si verifica uno spostamento proporzionale
a 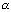 da
da
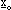 verso
verso
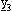 sino a raggiungere il punto
sino a raggiungere il punto
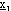 , che sarà così espresso:
, che sarà così espresso:

Se ora gli 8 nuovi punti nell’intorno di 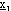 danno “insuccesso”, l’algoritmo ritorna in
danno “insuccesso”, l’algoritmo ritorna in 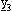 e da avvio ad una nuova “fase di esplorazione”, con un reticolo questa volta di lato
e da avvio ad una nuova “fase di esplorazione”, con un reticolo questa volta di lato
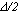 . Il processo di riduzione dei reticoli di
esplorazione continua fino a quando:
. Il processo di riduzione dei reticoli di
esplorazione continua fino a quando:

dove i è il numero di iterazioni continue senza “successo”. Quando tale limite viene
superato, si devono cercare altre strade di esplorazione.

Un’altra possibile alternativa, sempre restando fra i metodi diretti dove non si possiedono
informazioni sul gradiente, è tentarne un’approssimazione delle componenti attraverso rapporti
incrementali, ovvero esprimendo:
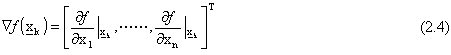
dove
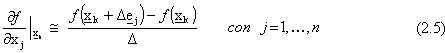
con 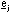 che rappresenta il versore della
componente j. A questo punto, pur di scegliere
che rappresenta il versore della
componente j. A questo punto, pur di scegliere
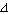 sufficientemente piccolo, ma a scapito
di una complessità computazionale non indifferente, si possono ottenere risultati paragonabili
con quelli dell’algoritmo del gradiente (presentato nel paragrafo 2.3).
sufficientemente piccolo, ma a scapito
di una complessità computazionale non indifferente, si possono ottenere risultati paragonabili
con quelli dell’algoritmo del gradiente (presentato nel paragrafo 2.3).
2.3 Metodi “basati sulla derivata prima”
Con metodi basati sulla derivata prima intendiamo quelle tecniche risolutive che,
conoscendo la forma analitica della funzione da minimizzare
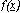 , utilizzano il gradiente (cioè le
derivate prime parziali) per giungere alla soluzione di un problema di programmazione non
lineare.
, utilizzano il gradiente (cioè le
derivate prime parziali) per giungere alla soluzione di un problema di programmazione non
lineare.
Quando 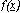 è nota e differenziabile,
utilizzare la condizione necessaria
è nota e differenziabile,
utilizzare la condizione necessaria 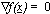 per l’esistenza del minimo equivale a costruire un sistema algebrico non lineare di n
equazioni e n incognite,
per l’esistenza del minimo equivale a costruire un sistema algebrico non lineare di n
equazioni e n incognite,

di solito estremamente arduo da risolvere. In questi casi, si preferisce ricorrere alle
tecniche di discesa (o di hill climbing), nelle quali si vuole determinare
una sequenza di punti 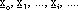 tali che
tali che

esprimibili inoltre nella forma:
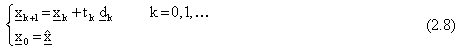
dove 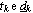 rappresentano rispettivamente la
lunghezza (positiva) e la direzione del passo di discesa. Considerando quindi la condizione
necessaria e sufficiente per avere la discesa:
rappresentano rispettivamente la
lunghezza (positiva) e la direzione del passo di discesa. Considerando quindi la condizione
necessaria e sufficiente per avere la discesa:

e sviluppando la serie di Taylor di 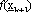 fino al 1° ordine, si ottiene:
fino al 1° ordine, si ottiene:

diseguaglianza che conduce a scegliere l’antigradiente come possibile direzione lungo la quale
effettuare il passo di discesa, ovvero a considerare

Da tutte queste considerazioni, possiamo ricavare l’algoritmo del gradiente nella nota
forma:
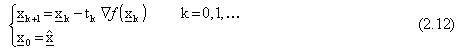
Nel caso (2.12) l’algoritmo è detto a passo ottimizzato, in quanto la lunghezza del
passo di discesa varia con k e può essere così scelta opportunamente ad ogni passo
attraverso una ricerca monodimensionale, minimizzando la seguente funzione rispetto
a 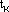 :
:

Un’alternativa al gradiente a passo ottimizzato, volendo evitare la ricerca ad ogni passo della
migliore lunghezza 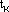 che assicura la discesa,
consiste nell’assegnare alla variabile una funzione decrescente con k, solitamente
espressa nella forma:
che assicura la discesa,
consiste nell’assegnare alla variabile una funzione decrescente con k, solitamente
espressa nella forma:

con 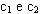 costanti da determinare. In questo
modo si arriva al gradiente a passo variabile non ottimizzato, buon compromesso fra
quello a passo ottimizzato e quello a passo fisso (che vedremo fra breve), soprattutto in
termini di convergenza e di complessità computazionale.
costanti da determinare. In questo
modo si arriva al gradiente a passo variabile non ottimizzato, buon compromesso fra
quello a passo ottimizzato e quello a passo fisso (che vedremo fra breve), soprattutto in
termini di convergenza e di complessità computazionale.
Quando invece la lunghezza del passo di discesa non varia con k, essendo una costante
nota a priori, siamo nel caso del gradiente a passo fisso (o gradiente puro),
esprimibile nella forma:
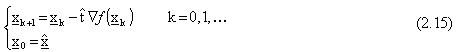
Qui la scelta di 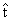 è critica:
con
è critica:
con 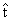 piccolo, la convergenza al punto
di minimo
piccolo, la convergenza al punto
di minimo 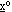 rischia di diventare troppo
lenta, mentre con
rischia di diventare troppo
lenta, mentre con 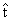 grande si possono
verificare “rimbalzi” che la impediscono.
grande si possono
verificare “rimbalzi” che la impediscono.
Si dimostra che, per funzioni 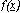 unimodali
(con un solo minimo locale), valgono le seguenti affermazioni:
unimodali
(con un solo minimo locale), valgono le seguenti affermazioni:
· l’algoritmo a passo fisso converge al punto di minimo pur di scegliere
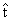 sufficientemente piccolo
sufficientemente piccolo
· l’algoritmo a passo ottimizzato converge sempre.
Per entrambi i casi possiamo utilizzare alcuni criteri di arresto che fermano
l’algoritmo non appena questo è vicino al minimo o il gradiente non subisce più significative
variazioni. Fra questi ricordiamo:
1) 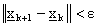
2) 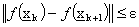
3) 
Dal momento che, in generale, non si conosce la forma analitica di
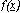 , conviene utilizzare l’AND
dei tre criteri, anziché uno in particolare.
, conviene utilizzare l’AND
dei tre criteri, anziché uno in particolare.
2.4 Metodi “basati sulla derivata seconda”
Con metodi basati sulla derivata seconda ci riferiamo a quelle tecniche capaci
di trovare la soluzione al problema di programmazione non lineare (2.1) utilizzando la
matrice Hessiana, avendo perciò a disposizione informazioni sulle derivate parziali seconde.
Uno dei più noti fra questi è l’algoritmo di Newton – Raphison nel quale, analogamente
al metodo del gradiente, si vuole determinare una sequenza di punti
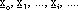 tale che:
tale che:

Supponendo ora 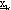 e
e
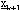 abbastanza vicini, possiamo
definire
abbastanza vicini, possiamo
definire 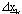 la distanza “infinitesima”
fra questi due punti, ottenendo cosi:
la distanza “infinitesima”
fra questi due punti, ottenendo cosi:

Sviluppando poi la serie di Taylor per 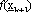 ,
attorno a
,
attorno a 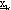 , fino al secondo ordine,
si ricava la forma quadratica
, fino al secondo ordine,
si ricava la forma quadratica

dove 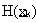 è la matrice Hessiana così
strutturata:
è la matrice Hessiana così
strutturata:
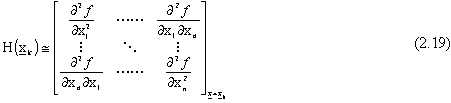
Essendo però l’approssimazione di 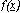 nell’intorno di
nell’intorno di 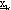 una forma quadratica,
risulta immediato determinare quel valore
una forma quadratica,
risulta immediato determinare quel valore 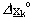 che la rende minima. Infatti si ha:
che la rende minima. Infatti si ha:

L’algoritmo di Newton - Raphison è così esprimibile nella forma:
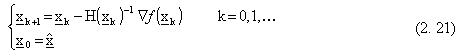
Questa tecnica consente convergenze al minimo molto veloci, fermo restando una notevole
complessità nel calcolo dell’hessiana e della sua inversa, che può rendere l’algoritmo
poco vantaggioso.
2.5 Addestramento Reti Neurali
Ritorniamo ora al problema iniziale, quello cioè di valutare quale sia fra i metodi di
programmazione non lineare esaminati quello più adatto a ottimizzare i pesi di una rete
approssimante, scegliendo di concentrare l’attenzione sul tipo “rete neurale feedforward”.
Come abbiamo visto nel primo capitolo, il processo di addestramento è riconducibile ad un
problema di programmazione non lineare nello spazio dei pesi, esprimibile quindi nella forma:

dove:

è il vettore colonna di tutti i pesi della rete, con
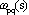 peso del neurone q del livello
s sull’uscita p del livello s-1, e J funzione di costo da
minimizzare.
peso del neurone q del livello
s sull’uscita p del livello s-1, e J funzione di costo da
minimizzare.
Si può subito notare come, data la dimensione solitamente grande del vettore dei pesi, un metodo
diretto risulti di non facile applicazione, essendo l’esplorazione dello spazio dei pesi
estremamente ardua.
Anche le tecniche che fanno ricorso alla matrice hessiana, quale l’algoritmo di
Newton-Raphison, pur garantendo una buona convergenza, sono insostenibili dal punto
di vista della complessità computazionale, in quanto richiedono il calcolo non sempre banale
delle derivate parziali seconde, oltre a quello dell’inversa della matrice stessa.
A condizionare ulteriormente l’impiego di queste tecniche, si aggiunge il fatto che la funzione
di costo solitamente contiene medie. Ad esempio, nel nostro utilizzo delle reti neurali come
approssimatori, J considera l’errore quadratico medio fra l’uscita della rete e il
valore vero della funzione valutata nei punti di addestramento.
Con il metodo del gradiente, invece, si può già ottenere una prima semplificazione dalla
scomposizione del gradiente della funzione di costo nel vettore colonna delle derivate
parziali rispetto ai singoli pesi, ovvero:
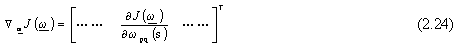
In questo modo si realizza l’importante concetto del calcolo distribuito, alla base
dell’algoritmo della “back propagation” per l’addestramento delle reti neurali, che ora
deriveremo dalle precedenti considerazioni.
Per calcolare la variazione del costo rispetto al singolo peso, una volta definita la quantità

si può applicare più volte la seguente derivazione “a catena”:

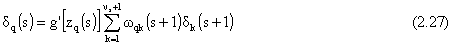
Il calcolo a ritroso delle 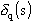 è cosi
inizializzato sullo strato di uscita:
è cosi
inizializzato sullo strato di uscita:

Calcolato il gradiente, si scende nella direzione dell’antigradiente per un numero di passi
sufficiente a raggiungere “error goal” desiderato.
Una alternativa all’algoritmo del gradiente, che consente una convergenza più rapida, è
l’approssimazione di Levenberg-Marquardt, ottenuta da una semplificazione del
metodo di Gauss – Newton ora descritto.
Il metodo di Gauss – Newton nasce come modifica all’algoritmo di Newton descritto
precedentemente, poco utilizzabile nella pratica per il calcolo oneroso dell’inversa della
matrice hessiana.
Nel caso dell’addestramento di una rete approssimante, il costo da minimizzare rispetto al
ettore di parametri 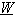 può essere
espresso nella forma
può essere
espresso nella forma

dove:
· 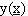 è la generica funzione da approssimare
è la generica funzione da approssimare
·  è l’l-esimo punto del
“training set”
è l’l-esimo punto del
“training set”
· 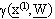 è il valore della funzione
approssimante nell’l-esimo punto del “training set”
è il valore della funzione
approssimante nell’l-esimo punto del “training set”
· 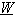 è il vettore dei parametri sui
quali vogliamo effettuare la minimizzazione.
è il vettore dei parametri sui
quali vogliamo effettuare la minimizzazione.
Se definiamo ora il vettore errore relativo rispetto al singolo punto l di
addestramento

e il vettore globale

allora il costo è così esprimibile:
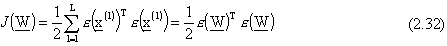
Per funzioni quadratiche in 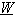 il metodo
di Newton assicura la convergenza in un solo passo. Per rendere la funzione
il metodo
di Newton assicura la convergenza in un solo passo. Per rendere la funzione
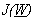 quadratica in
quadratica in
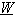 , si può usare un approssimatore
lineare nei parametri:
, si può usare un approssimatore
lineare nei parametri:

dove 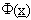 è un’opportuna funzione,
in modo tale che gli errori di approssimazione
è un’opportuna funzione,
in modo tale che gli errori di approssimazione 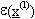 ,
e conseguentemente
,
e conseguentemente 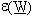 , siano anch’essi
lineari rispetto a
, siano anch’essi
lineari rispetto a 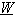 , e quindi il costo
risulti quadratico in
, e quindi il costo
risulti quadratico in 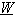 , come evidente
in (2.32).
, come evidente
in (2.32).
L’uso, invece, di approssimatori 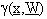 non
lineari nei parametri comporta non linearità in
non
lineari nei parametri comporta non linearità in 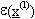 e quindi in
e quindi in 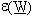 . Per poter impiegare
approssimatori di questo tipo, l’approccio di Gauss – Newton suggerisce di procedere,
ad ogni iterazione j dell’algoritmo, secondo i seguenti passi:
. Per poter impiegare
approssimatori di questo tipo, l’approccio di Gauss – Newton suggerisce di procedere,
ad ogni iterazione j dell’algoritmo, secondo i seguenti passi:
1) linearizzare l’errore 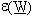 intorno al
valore corrente di
intorno al
valore corrente di 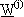
2) risolvere un problema ai minimi quadrati per minimizzare l’errore e fissare di conseguenza
il successivo valore dei parametri 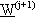 .
.
Rispetto al classico metodo di Newton, qui si costruisce ad ogni iterazione un’approssimazione
quadratica della funzione da minimizzare, operando attraverso una linearizzazione, anziché
utilizzare informazioni relative alla derivata seconda.
Nella prima fase, la linearizzazione di 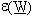 attorno a
attorno a 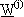 è realizzata mediante
un’espansione in serie di Taylor troncata al termine lineare, che porta l’errore globale
ad assumere la forma:
è realizzata mediante
un’espansione in serie di Taylor troncata al termine lineare, che porta l’errore globale
ad assumere la forma:
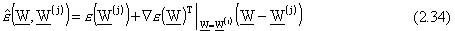
dove 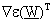 è la matrice jacobiana.
è la matrice jacobiana.
Nella seconda fase invece, una volta minimizzata la norma quadra della funzione precedentemente
linearizzata e ottenuto

si arriva, analogamente al caso con funzione approssimante lineare nei parametri, al seguente
problema di minimizzazione ai minimi quadrati, che consente di determinare il successivo valore
dei parametri:
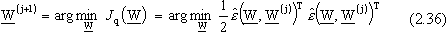
Ricordiamo che, nel caso di approssimatore lineare, si pone

mentre nel caso in esame si ottiene:
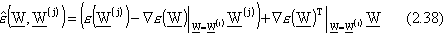
A questo punto, con le due assegnazioni:


possiamo determinare il 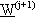 per la (2.36),
anche nel caso di funzione approssimante non lineare nei parametri, con la nota formula
risolutiva per il problema della stima ai minimi quadrati.
per la (2.36),
anche nel caso di funzione approssimante non lineare nei parametri, con la nota formula
risolutiva per il problema della stima ai minimi quadrati.
La regola di aggiornamento dei pesi secondo Gauss – Newton diventa perciò la seguente:
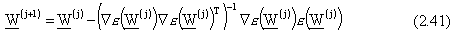
con:

Con il metodo di Gauss – Newton si ottiene una convergenza tipicamente più veloce di quella
ottenuta con il metodo del gradiente, ma in generale non così veloce come con il metodo di
Newton puro, fermo restando un minore onere computazionale per l’assenza del calcolo
dell’hessiana.
Nonostante ciò, per ovviare anche al problema del calcolo dell’inversa nella (2.41), spesso
si ricorre alla seguente regola di aggiornamento:
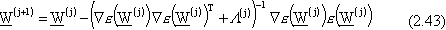
dove 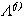 è una matrice diagonale tale che
la quantità da invertire fra parentesi tonde sia definita positiva.
Nell’approssimazione di Levemberg–Marquardt si sceglie
è una matrice diagonale tale che
la quantità da invertire fra parentesi tonde sia definita positiva.
Nell’approssimazione di Levemberg–Marquardt si sceglie
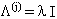 , con
, con
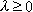 e I matrice identica di
dimensione p.
e I matrice identica di
dimensione p.
In questo modo il parametro 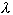 consente
di selezionare il tipo di discesa che si vuole effettuare. In particolare, quando
consente
di selezionare il tipo di discesa che si vuole effettuare. In particolare, quando
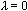 l’equazione (2.43) riporta esattamente
la regola di cambiamento dei pesi del metodo di Gauss-Newton. Quanto più cresce
l’equazione (2.43) riporta esattamente
la regola di cambiamento dei pesi del metodo di Gauss-Newton. Quanto più cresce
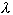 , tanto più la direzione di discesa
si avvicina a quella del metodo del gradiente. Quindi, in generale, per piccoli valori di
, tanto più la direzione di discesa
si avvicina a quella del metodo del gradiente. Quindi, in generale, per piccoli valori di
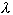 possiamo aspettarci una convergenza
veloce, mentre per alti valori di
possiamo aspettarci una convergenza
veloce, mentre per alti valori di 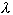 otterremo una convergenza più lenta.
otterremo una convergenza più lenta.
Riassumendo, dal momento che il metodo di Gauss-Newton risulta più veloce e accurato in
prossimità di un valore minimo del costo, si fa in modo che
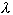 diminuisca dopo ogni passo in cui
si consegua una discesa e aumenti quando un passo dell’algoritmo non abbia successo e si salga.
Si ottiene così un automatico passaggio al metodo più conveniente di caso in caso.
diminuisca dopo ogni passo in cui
si consegua una discesa e aumenti quando un passo dell’algoritmo non abbia successo e si salga.
Si ottiene così un automatico passaggio al metodo più conveniente di caso in caso.

Ringraziamenti,
Introduzione,
Capitolo 1,
Capitolo 2,
Capitolo 3,
Capitolo 4,
Bibliografia

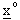 capace di minimizzare la funzione data.
capace di minimizzare la funzione data.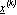 è il punto di minimo al k-esimo
tentativo e
è il punto di minimo al k-esimo
tentativo e 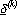 lo spostamento estratto
casualmente che porta in
lo spostamento estratto
casualmente che porta in 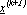 , l’algoritmo può
essere così schematizzato:
, l’algoritmo può
essere così schematizzato: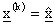
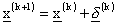
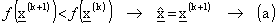 , altrimenti (b) con una nuova
estrazione dello spostamento
, altrimenti (b) con una nuova
estrazione dello spostamento 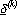 .
.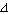
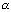
 .
.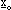 che formano un quadrato di lato
che formano un quadrato di lato
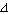 intorno ad esso, fino a quando non trova
il punto
intorno ad esso, fino a quando non trova
il punto 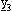 in cui
in cui
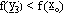 : termina così la prima fase.
: termina così la prima fase.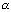 da
da
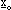 verso
verso
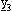 sino a raggiungere il punto
sino a raggiungere il punto
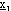 , che sarà così espresso:
, che sarà così espresso:
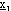 danno “insuccesso”, l’algoritmo ritorna in
danno “insuccesso”, l’algoritmo ritorna in 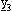 e da avvio ad una nuova “fase di esplorazione”, con un reticolo questa volta di lato
e da avvio ad una nuova “fase di esplorazione”, con un reticolo questa volta di lato
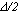 . Il processo di riduzione dei reticoli di
esplorazione continua fino a quando:
. Il processo di riduzione dei reticoli di
esplorazione continua fino a quando:

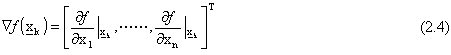
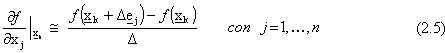
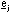 che rappresenta il versore della
componente j. A questo punto, pur di scegliere
che rappresenta il versore della
componente j. A questo punto, pur di scegliere
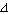 sufficientemente piccolo, ma a scapito
di una complessità computazionale non indifferente, si possono ottenere risultati paragonabili
con quelli dell’algoritmo del gradiente (presentato nel paragrafo 2.3).
sufficientemente piccolo, ma a scapito
di una complessità computazionale non indifferente, si possono ottenere risultati paragonabili
con quelli dell’algoritmo del gradiente (presentato nel paragrafo 2.3).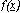 , utilizzano il gradiente (cioè le
derivate prime parziali) per giungere alla soluzione di un problema di programmazione non
lineare.
, utilizzano il gradiente (cioè le
derivate prime parziali) per giungere alla soluzione di un problema di programmazione non
lineare.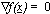 per l’esistenza del minimo equivale a costruire un sistema algebrico non lineare di n
equazioni e n incognite,
per l’esistenza del minimo equivale a costruire un sistema algebrico non lineare di n
equazioni e n incognite,
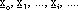 tali che
tali che
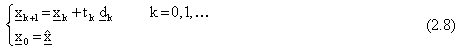
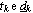 rappresentano rispettivamente la
lunghezza (positiva) e la direzione del passo di discesa. Considerando quindi la condizione
necessaria e sufficiente per avere la discesa:
rappresentano rispettivamente la
lunghezza (positiva) e la direzione del passo di discesa. Considerando quindi la condizione
necessaria e sufficiente per avere la discesa:
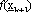 fino al 1° ordine, si ottiene:
fino al 1° ordine, si ottiene:

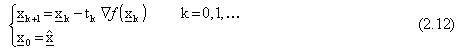
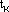 :
:

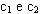 costanti da determinare. In questo
modo si arriva al gradiente a passo variabile non ottimizzato, buon compromesso fra
quello a passo ottimizzato e quello a passo fisso (che vedremo fra breve), soprattutto in
termini di convergenza e di complessità computazionale.
costanti da determinare. In questo
modo si arriva al gradiente a passo variabile non ottimizzato, buon compromesso fra
quello a passo ottimizzato e quello a passo fisso (che vedremo fra breve), soprattutto in
termini di convergenza e di complessità computazionale.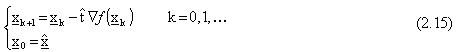
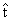 è critica:
con
è critica:
con 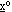 rischia di diventare troppo
lenta, mentre con
rischia di diventare troppo
lenta, mentre con 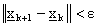
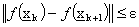


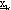 e
e
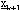 abbastanza vicini, possiamo
definire
abbastanza vicini, possiamo
definire 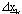 la distanza “infinitesima”
fra questi due punti, ottenendo cosi:
la distanza “infinitesima”
fra questi due punti, ottenendo cosi:

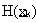 è la matrice Hessiana così
strutturata:
è la matrice Hessiana così
strutturata: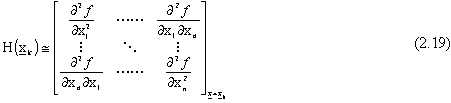
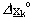 che la rende minima. Infatti si ha:
che la rende minima. Infatti si ha:
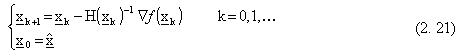


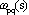 peso del neurone q del livello
s sull’uscita p del livello s-1, e J funzione di costo da
minimizzare.
peso del neurone q del livello
s sull’uscita p del livello s-1, e J funzione di costo da
minimizzare.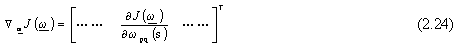


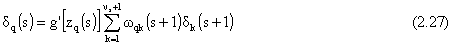
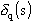 è cosi
inizializzato sullo strato di uscita:
è cosi
inizializzato sullo strato di uscita:
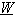 può essere
espresso nella forma
può essere
espresso nella forma
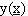 è la generica funzione da approssimare
è la generica funzione da approssimare è l’l-esimo punto del
“training set”
è l’l-esimo punto del
“training set”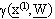 è il valore della funzione
approssimante nell’l-esimo punto del “training set”
è il valore della funzione
approssimante nell’l-esimo punto del “training set”

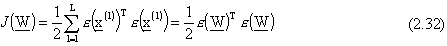
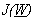 quadratica in
quadratica in

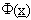 è un’opportuna funzione,
in modo tale che gli errori di approssimazione
è un’opportuna funzione,
in modo tale che gli errori di approssimazione 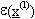 ,
e conseguentemente
,
e conseguentemente 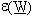 , siano anch’essi
lineari rispetto a
, siano anch’essi
lineari rispetto a 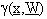 non
lineari nei parametri comporta non linearità in
non
lineari nei parametri comporta non linearità in 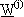
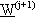 .
.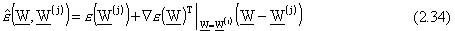
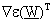 è la matrice jacobiana.
è la matrice jacobiana.
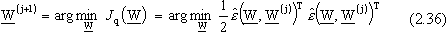

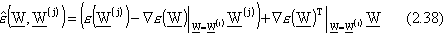


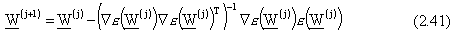

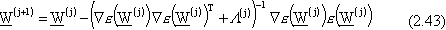
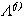 è una matrice diagonale tale che
la quantità da invertire fra parentesi tonde sia definita positiva.
Nell’approssimazione di Levemberg–Marquardt si sceglie
è una matrice diagonale tale che
la quantità da invertire fra parentesi tonde sia definita positiva.
Nell’approssimazione di Levemberg–Marquardt si sceglie
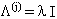 , con
, con
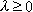 e I matrice identica di
dimensione p.
e I matrice identica di
dimensione p.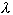 consente
di selezionare il tipo di discesa che si vuole effettuare. In particolare, quando
consente
di selezionare il tipo di discesa che si vuole effettuare. In particolare, quando
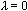 l’equazione (2.43) riporta esattamente
la regola di cambiamento dei pesi del metodo di Gauss-Newton. Quanto più cresce
l’equazione (2.43) riporta esattamente
la regola di cambiamento dei pesi del metodo di Gauss-Newton. Quanto più cresce