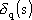CAPITOLO 3
Implementazione Software
3.1 Dal modello alla sua implementazione
Nei capitoli precedenti abbiamo introdotto il modello computazionale delle reti approssimanti,
focalizzando poi la nostra attenzione sulle loro proprietà approssimanti e su alcune classi di
reti, in particolare le reti neurali. Da tutto ciò sono emerse le loro potenzialità soprattutto
nella risoluzione di problemi poco formalizzabili da un punto di vista algoritmico, ma facilmente
descrivibili qualitativamente.
Ci chiediamo ora come sia possibile passsare dal modello “astratto” al corrispondente “reale” o
“implementato” su elaboratore, per definire e successivamente risolvere tale classe di problemi.
Si vuole perciò realizzare un “ambiente software”, capace in primo luogo di gestire la struttura
dati rete neurale e di fornire quelle funzioni neccessarie alla sua costruzione, inizializzazione
e al suo addestramento, e in secondo luogo di sposare l’efficienza di calcolo con la facilità di
utilizzo da parte dell’utente (due aspetti che verranno presi in considerazione soprattutto per
le future applicazioni). Abbiamo scelto a tale scopo due “filosofie” di programmazione “opposte”:
Matlab e C.
Nel primo capitolo si è visto che la j-esima componente di una rete approssimante può
essere così caratterizzata:

dove 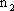 è la dimensione della funzione da
approssimare,
è la dimensione della funzione da
approssimare, 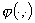 è una data funzione base,
mentre i
è una data funzione base,
mentre i 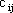 e le componenti di
e le componenti di
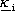 sono i parametri da determinare,
esprimibili anche come unico vettore
sono i parametri da determinare,
esprimibili anche come unico vettore
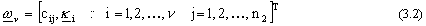
Nel seguito ci limiteremo a trattare una classe particolare di reti, cioé le multilayer
feedforward networks, la cui struttura è rappresentata in figura 1-2, per via della loro
“popolarità” e del buon numero di risultati teorici disponibili.
Possiamo notare che, indipendentemente dalle scelte implementative e dal linguaggio di
programmazione utilizzato, il tipo di dato rete neurale deve senz’altro includere le seguenti
informazioni:
· ingressi alla rete
· numero dei livelli o degli strati (solitamente sono due, il primo è lo strato
nascosto, il secondo lo strato di uscita)
· numero dei neuroni per livello
· tipo funzione di attivazione che caratterizza i neuroni di un livello
· pesi di ogni livello
· uscite di ogni livello
· uscite della rete.
Sulla base di queste considerazioni, possiamo osservare che:
a) gli ingressi del primo livello corrispondono agli ingressi della rete
b) le uscite di ogni livello rappresentano gli ingressi del livello successivo
c) le uscite della rete sono le uscite dell’ultimo livello
d) i pesi e le uscite che caratterizzano ogni strato possono essere distribuiti
fra i suoi neuroni costituenti (in questo modo al singolo neurone viene assegnato
un vettore dei pesi, comprendente il suo bias e i pesi sulle uscite del livello
precedente).
Assegnati quindi alla nuova struttura dati rete neurale questi attributi, si vogliono realizzare
quelle funzioni necessarie al suo ciclo di vita ed in particolare quelle strettamente legate
all’agoritmo della back-propagation, scelto come metodo di addestrameto, quali:
· costruttore
· distruttore (se necessario)
· inizializzatore dei pesi
· fase forward
· fase backward
· lettura su file
· scrittura su file
Nei successivi paragrafi, dopo una breve presentazione dei due linguaggi di programmazione,
saranno presentati per le reti neurali feed-forward due modelli alternativi, ma comunque
equivalenti, che si rifanno ai requisiti appena elencati, implementati rispettivamente in
Matlab e in C, specificando ove necessario l’eventuale presenza del “software di contorno”
indispensabile alla loro realizzazione.
3.2 Matlab e C a confronto
La scelta di un determinato linguaggio di programmazione può risultare strategica per il successo
o il fallimento di un prodotto software.
In questo paragrafo saranno brevemente descritte le principali caratteristiche di Matlab e del C,
i due linguaggi scelti come “ambienti” per lo sviluppo di software sulle reti neurali.
Matlab, da Matrix Laboratory, è un interprete di comandi che, grazie al suo ricco
ambiente di sviluppo integrato, offre tutte le possibilità di un vero e proprio linguaggio
di programmazione. È capace di integrare il calcolo, la visualizzazione e la programmazione
in un ambiente di facile utilizzo, dove i problemi e le soluzioni sono espresse in una
notazione matematica familiare.
Matlab è un sistema interattivo il cui tipo base elementare è l’array (vettore) che
non richiede di essere dimensionato. Ciò consente di risolvere molti problemi di calcolo,
specialmente quelli con matrici e vettori, e di formularli in una maniera molto più veloce di
quella che richiederebbe un programma scritto in Fortran o C, linguaggi per nulla interattivi.
Inoltre nelle ultime versioni possiamo trovare il cell-array, nuovo tipo base che
consente di realizzare strutture complesse, caratterizzate dalla presenza di variabili
differenti, oltre che nel tipo, anche nella dimensione.
Per questi motivi, Matlab è un linguaggio di alte performance per il calcolo matematico,
tipicamente utilizzato per lo sviluppo di algoritmi, la modellazione, la simulazione e la
costruzione di prototipi, l’analisi dei dati e la visualizzazione, per la costruzione di
interfacce grafiche utente.
Bisogna sottolineare poi come esso si sia evoluto nel corso degli anni grazie agli utenti
che hanno contribuito, sia in campo universitario sia in quello industriale, all’implementazione
di nuove funzioni. Matlab è caratterizzato così da una famiglia di soluzioni per applicazioni
specifiche, chiamati toolboxes, che consentono di apprendere e sviluppare determinati
problemi, essendo una collezione di funzioni (definite negli m-file) che estentono l’ambiente
Matlab e lo rendono in grado di risolvere particolari classi di problemi.
Le aree nelle quali i toolboxes sono disponibili includono fra le altre signal processing,
control systems, reti neurali, fuzzy logic, simulazione.
Grazie a tutto ciò, Matlab consente sia la “programming in the small” per creare rapidamente
veloci programmi sia la “programming in the large” per applicazioni più complesse.
I motivi per cui abbiamo scelto di sviluppare “ex novo” un pacchetto software per la gestione
delle reti neurali sono dovuti principalmente al fatto che, nelle nostre applicazioni, occorre
una certa flessibilità nell’utilizzo dell’algoritmo della “back propagation”, dovuta alla presenza
del gradiente stocastico, e ciò non è consentito dal toolbox, per altri aspetti molto completo,
di Matlab. Non abbiamo scelto infatti di implementare l’approssimazione di Levemberg -
Marquardt,
tecnica effettivamente molto usata per l’addestramento delle reti neurali, proprio perché
il toolbox dispone di una sua realizzazione molto efficiente.
Per una più completa panoramica sulle caratteristiche e sulle potenzialità di Matlab rimandiamo,
per esempio, a [8] e [9].
Per quel che riguarda il C, esso è un passo al di sopra rispetto ai linguaggi orientati
alle macchine, o di basso livello, ma un passo al di sotto dei linguaggi risolutori
di problemi, o di alto livello, essendo abbastanza vicino al computer da fornire un grande
controllo sui dettagli implementativi di un’applicazione, ma abbastanza lontano da poter ignorare
i dettagli dell’hardware.
Nel C vi sono molte meno regole di sintassi che in altri linguaggi ed è così possibile scrivere
un compilatore C di alta qualità che funzioni in soli 256K di memoria totale.
Il C possiede un insieme conciso di parole chiave e, ad esempio, non contiene alcuna funzionalità
integrata di input e output, funzioni per il trattamento delle stringhe o per l’accesso al file
system. Dispone però di un ricco insieme di funzioni di libreria, usato con tale frequenza e
normalità da poter essere considerato quasi come parte integrante del linguaggio stesso.
Vi sono librerie per funzioni matematiche, elementi grafici, trattamento dei file, supporto
di database, realizzazione di finestre sullo schermo, immissione di dati, comunicazioni e
funzioni generiche di supporto.
Oltre a consentire l’allocazione dinamica della memoria e la possibilità di indirizzare
particolari aree di memoria, il C si distingue dagli altri linguaggi di programmazione
perché è l’unico a realizzare un’aritmetica dei puntatori che permette una gestione più
semplice di tali variabili.
Il codice C prodotto dalla maggior parte dei compilatori è molto efficiente. La ristrettezza
del linguaggio, le ridotte dimensioni del sistema run-time, l’uso dei puntatori ed il fatto
che il linguaggio sia vicino all’hardware fanno sì che molti programmi in C siano eseguiti a
velocità vicine a quelle degli equivalenti programmi scritti in linguaggi
assembler.
Il C supporta la programmazione modulare, dove compilazione e linking sono separate, che
consente di ricompilare solo le parti del programma aggiornate durante lo sviluppo. Tale
caratteristica può essere estremamente importante quando si sviluppano programmi di grandi
dimensioni o anche programmi di media grandezza su sistemi lenti. Senza il supporto della
programmazione modulare, la quantità di tempo necessaria per compilare un programma completo
potrebbe rendere il ciclo di compilazione, collaudo e modifica assai lento. Il C è inoltre
un linguaggio non fortemente tipizzato, in quanto offre una grande flessibilità nel manipolare
i dati. Questo consente ad esempio di visualizzare i dati in formato diverso o di eseguire
operazioni di casting, ma anche di scrivere espressioni con valori non precisamente definiti,
che possono causare errori imprevedibili a run-time. Per ulteriori chiarimenti sul C,
si veda [10].
Per la realizzazione del nostro modello, se da una parte abbiamo scelto Matlab per la sua
“immediatezza” o facilità nella gestione di strutture dati complesse, quali che sono le reti
neurali, dall’altra abbiamo deciso di impiegare il C per la sua potenza nello sviluppo di
programmi eseguibili efficienti, oltre naturalmente alle motivazioni già discusse a riguardo
dell’implementazione del gradiente stocastico.
3.3 Matlab e le reti neurali
Abbiamo già visto nel primo capitolo come la struttura della j-esima componente di una rete
feedforward possa essere così definita:
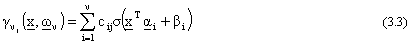
Dal momento che le informazioni caratterizzanti una rete neurale sono di vario formato e di
dimensioni spesso variabili (vedi paragrafo 3.1), nell’implementare in Matlab la struttura
dati principale del modello si è scelto di ricorrere al cell-array, addottando perciò una
visione di insieme.
In esso le singole celle contengono rispettivamente:
· numero dei livelli L
· struttura della rete N (cell-array in cui compaiono nell’ordine il numero degli
ingressi della rete e, per ogni livello, la coppia numero di neuroni – tipo funzione di
attivazione)
· ingressi parziali Z (cell-array nel quale si trovano L vettori, uno per
ogni livello s della rete, le cui componenti rappresentano l’ingresso pesato totale
al singolo neurone del livello s)
· uscite parziali Y (cell-array che include il vettore degli ingressi alla rete nella
prima cella, i vettori delle uscite di ogni livello s nelle successive)
· pesi della rete W (cell-array costituito da L matrici bidimensionali, nelle
quali sono contenuti i pesi di ogni livello).
Va subito precisato che le matrici bidimensionali dei pesi hanno m colonne pari al
numero dei neuroni del livello s cui si riferiscono e n righe pari al numero
delle uscite del livello s-1 maggiorato però di 1, per considerare tutti i bias del
livello s.
Definendo in questo modo una rete neurale, in Matlab è stato possibile attraverso solo quattro
funzioni implementare l’intero suo ciclo di vita, dalla sua costruzione e inizializzazione,
sino al suo addestramento.
La funzione costruttrice buildnet è così responsabile della definizione delle proprietà
strutturali della rete. Essa riceve in ingresso la dimensione del vettore degli ingressi, seguito
da una lista di lunghezza variabile di argomenti formata dalle coppie nemero neuroni – tipo
funzione di attivazione che caratterizzano i singoli livelli, inizializzando quindi le celle
L e N.
Effettuando, ad esempio, la seguente chiamata:
rete = buildnet(2,100,’logsig’,2,’purelin’)
possiamo creare una rete feedforward a due strati, con 2 ingressi, 100 neuroni logsig
nel primo livello e 2 neuroni purelin nel secondo.
A questo punto la funzione initnet può determinare le dimensioni delle matrici dei
pesi corrispondenti a ciascun livello, che andranno a costituire il cell-array W.
Essa prende perciò come argomenti la rete stessa e il range di estrazione casuale dei pesi,
restituendo poi la rete i cui pesi sono stati inizializzati nel dominio specificato, come
risulta chiaro dalla chiamata:
new_rete = initnet(old_rete,1)
che inizializza i pesi di old_rete in [-1,1], restituendo poi new_rete.
Per applicare ora alla rete neurale un vettore di ingresso e calcolare la corrispondente
uscita (fase forward della back-propagation), si rende necessario completarne la struttura
con l’introduzione degli ingressi e delle uscite parziali, ovvero dei cell-array Z
e Y.
La funzione forward svolge proprio questo compito. Riceve il vettore degli ingressi
con la rete già inizializzata e produce l’uscita della rete, senza ovviamente modificare in
alcun modo i pesi della rete, costruendo e inizializzando livello dopo livello i vettori
degli ingressi e delle uscite parziali, come possiamo capire dal seguente esempio:
[new_rete, outputs] = forward(old_rete, [0.3 –0.6]’)
dove il vettore degli ingressi [0.3 –0.6] viene applicato a old_rete e l’uscita corrispondente
restituita nel vettore outputs.
Per ogni neurone q del livello s viene dapprima calcolato l’ingresso pesato
totale, quindi la corrispondente uscita, applicando ad esso la funzione di attivazione che lo
caratterizza.
È importante notare qui l’efficenza della funzione Matlab feval, utilizzata all’interno
della forward per determinare l’uscita di ogni singolo neurone, che consente ad esempio
di passare ad una funzione matematica uno o più argomenti di dimensione variabile (scalari,
vettori o matrici).
Occorre inoltre precisare che, per caratterizzare i neuroni del nostro modello, sono stati presi
in considerazione i seguenti quattro tipi funzione di attivazione fra quelli forniti da
Matlab:
· 
· 
· 
· 
L’ultima funzione implementata, fondamentale nelle applicazioni che utilizzano le reti neurali
perché responsabile dell’aggiornamento dei pesi dell’intera struttura, è la backward:
in essa viene codificata la seconda fase dell’algoritmo della back-propagation, nella quale si
verifica col metodo del gradiente un passo di discesa nello spazio dei pesi.
Ricordiamo, a questo proposito, come il calcolo delle derivate parziali costituenti il gradiente
possa essere così espresso:

dove le 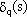 sono calcolate “a ritroso” per
mezzo della (3.9)
sono calcolate “a ritroso” per
mezzo della (3.9)
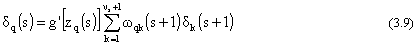
Per ottenere ciò, la backward riceve in ingresso:
· la rete inizializzata o frutto di un precedente addestramento
· la lunghezza del passo di discesa
· il vettore delle derivate parziali del costo rispetto alle uscite dell’ultimo livello
e restituisce:
· la rete con le matrici dei pesi aggiornate
· il vettore delle derivate parziali del costo rispetto agli ingressi.
Una tipica chiamata alla funzione backward è perciò la seguente:
[dJy0, new_rete] = backward(old_rete,[1.2 –0.6],0.05)
che aggiorna i pesi di old_rete attraverso un passo di discesa dell’algoritmo del gradiente
(0.05 è la lunghezza del passo), restituendo in dJy0 il vettore delle derivate parziali del
costo rispetto agli ingressi.
Nello sviluppo di questa procedura, si sono apprezzate da una parte la possibilità offerta
da Matlab di esprimere le formule matematiche in notazione “standard” e dall’altra l’enorme
compattezza delle stesse.
È stato infatti possibile implementare con estrema velocità sia il calcolo a ritroso delle
 sia l’algoritmo del gradiente per
l’aggiornamento dei pesi, dal momento che l’ambiente consente di chiamare le funzioni anche
su argomenti strutturati (vettori, matrici o cell-array).
sia l’algoritmo del gradiente per
l’aggiornamento dei pesi, dal momento che l’ambiente consente di chiamare le funzioni anche
su argomenti strutturati (vettori, matrici o cell-array).
Ad esempio, per valutare le  di un dato
livello s della rete, sono sufficienti le due seguenti righe di codice:
di un dato
livello s della rete, sono sufficienti le due seguenti righe di codice:
dJz{s} = dgz'.*dJy{s} ;
dJw{s} = [1;y{s-1}(:,1)]*(dJz{1,s}).
Vedremo più avanti che il C non permette una codifica così rapida e compatta. Per quanto
riguarda infine la lettura da file o la scrittura su file dello “stato” di una rete neurale,
aspetto molto importante perchè spesso si vuole riprendere un vecchio addestramento o eseguire
una fase di simulazione, è sufficiente ricorrere rispettivamente alle funzioni Matlab
load e save che consentono un accesso immediato al file system.
3.4 C e le reti neurali
Al contrario di Matlab, dove il tipo base array e quello più evoluto cell-array
hanno consentito di definire quasi “istantaneamente” la rete neurale, in C si è resa necessaria
una fase preliminare di implementazione, allo scopo di dotare l’ambiente delle strutture dati
indispensabili al modello.
Inoltre, non essendo possibile già in compilazione definire variabili statiche (ad esempio vettori)
senza specificarne la dimensione, nella maggior parte dei casi si è fatto ricorso all’allocazione
dinamica della memoria.
Ciò, se da una parte ha garantito un uso efficiente e “diretto” delle variabili con un controllo
pressoché totale su di esse, velocizzando notevolmente l’esecuzione dei programmi, dall’altra ha
rallentato e esteso non di poco l’implementazione/debugging del codice, dovendo questo anche
garantire la massima portabilità rispetto alle “piattaforme” UNIX e MS-DOS.
Ritornando ora al problema dei tipi base sui quali verrà costruita la nostra rete neurale, abbiamo
dovuto realizzare alcune strutture dati indispensabili al modello, quali i vettori, le matrici,
gli insiemi di vettori e gli insiemi di matrici, ricorrendo alle liste dinamicamente linkate.
Un vettore è così caratterizzato da una dimensione n e da un puntatore alla lista degli
n elementi. I costruttori vet_i_allc_ini, vet_l_allc_ini e
vet_d_allc_ini allocano lo spazio di memoria necessario a contenere n valori di
interi, long o double rispettivamente, mentre i distruttori vet_d_free, vet_i_free
e vet_l_free liberano la memoria precedentemente allocata. La funzione vet_d_init
inizializza casualmente gli elementi di un “vettore double”.
Una matrice è invece costituita dal numero delle righe r, dal numero delle colonne
c e da un doppio puntatore ad una lista di n×c elementi. Le funzioni
mat_i_allc_ini o mat_d_allc_ini sono i costruttori, mentre mat_d_free
o mat_i_free i distruttori, rispettivamente nel caso di elementi interi o double.
Come vedremo poi nel capitolo 4, la definizione degli insiemi di vettori o di matrici si rende
necessaria per alcuni tipi di applicazione sulle reti neurali, anche se non rientra nella loro
struttura.
Un insieme di vettori risulta perciò formato dai seguenti campi: numero dei vettori, loro
dimensione e corrispondente lista. Un insieme di matrici è strutturato in maniera analoga,
anche se qui occorre specificare due dimensioni, ovvero il numero delle righe e delle colonne.
Entrambi gli “oggetti” poi dispongono di funzioni per la loro costruzione, inizializzazione
casuale e distruzione, che ovviamente si basano su quelle appena viste per vettori e matrici.
Dopo tutte queste premesse, per arrivare alla realizzazione della rete neurale del nostro modello,
in C si è preferito partire dalla definizione del neurone, quale suo elemento base, di cui la
figura 3-1 ne riporta la struttura.
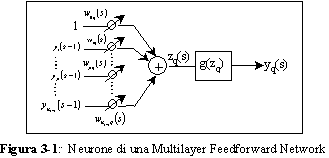
Un neurone può essere così definito dai seguenti campi:
· ingresso z
· uscita y
· vettore dei pesi 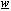 .
.
L’informazione sul tipo di funzione di attivazione g che caratterizza il neurone
(scelta fra le logsig, tansig, radbas e purelin citate
nel paragrafo 3.3) e che applicata all’ingresso z produce l’uscita y qui
non compare, essendo più direttamente legata al suo livello di appartenenza.
Con l’introduzione fra breve dei livelli, il vettore 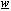 dei pesi del neurone q nel livello s dovrà contenere
dei pesi del neurone q nel livello s dovrà contenere
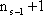 scalari double, ovvero gli
scalari double, ovvero gli
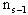 pesi sulle uscite del livello precedente
s-1, oltre al bias, e quindi sarà esprimibile come:
pesi sulle uscite del livello precedente
s-1, oltre al bias, e quindi sarà esprimibile come:
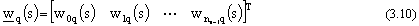
Ciò consentirà quindi di determinare il valore z dell’ingresso pesato e dell’uscita
y corrispondente (entrambi double), applicando le note relazioni
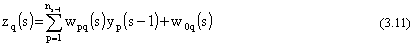

Per gestire ora questo tipo di dato, sono stati implementati il costruttore nalloc e
il distruttore de_nalloc (libreria neu_mem.h) che si occupano di allocare o
deallocare rispettivamente uno spazio di memoria sufficiente a contenere un certo numero di
neuroni.
Sfruttando ora i tipi precedentemente introdotti e considerando l’analisi dei requisiti minimi
fatta sul modello (vedi paragrafo 3.1), si giunge alla formulazione della struttura dati rete
neurale in termini di:
· numero dei livelli
· numero degli ingressi
· numero delle uscite
· massimo numero di neuroni fra i livelli
· numero di neuroni per livello (vettore di interi le cui componenti indicano da quanti neuroni
è formato un livello)
· tipo funzione di attivazione per livello (vettore di interi che contiene per ogni livello il
codice della funzione attivazione, ovvero 1 per logsig, 2 per tansig, 3 per
radbas e 4 per purelin)
· insieme di neuroni (array bidimensionale di puntatori a neurone, dove l’elemento
[s,q] rappresenta il neurone q del livello s).
Naturalmente, per i nostri scopi, una rete neurale necessita sì del costruttore ralloc
e del distruttore de_ralloc, responsabili dell’allocazione dinamica della struttura,
ma anche di molte altre funzioni che permettano di inizializzarne i campi (numero ingressi,
numero livelli, ...) e di compiere fasi successive di addestramento per ottimizzarne i pesi.
La prima funzione che analizziamo è la build_net. Essa si occupa di dare inizialmente
alla rete neurale una certa “fisionomia”, definendone il numero dei livelli, il numero di neuroni
e il tipo di funzione di attivazione per livello, e quindi di allocare per ogni neurone un vettore
dei pesi 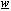 delle giuste dimensioni. Per fare
ciò riceve in ingresso la rete precedentemente allocata, il numero degli ingressi, i vettori del
numero di neuroni e del tipo di funzione di attivazione per livello, come si può vedere dal suo
prototipo:
delle giuste dimensioni. Per fare
ciò riceve in ingresso la rete precedentemente allocata, il numero degli ingressi, i vettori del
numero di neuroni e del tipo di funzione di attivazione per livello, come si può vedere dal suo
prototipo:
void build_net (NN *rete, int nlivelli, VET_INT *neu_vet, VET_INT *neu_functions)
Init_net invece inizializza i pesi della rete, o estraendoli casualmente nel range
specificato o caricandoli da file e, per fare ciò, accetta in ingresso la rete già “strutturata”,
il file dei pesi e un parametro booleano che indica se utilizzare tale file, come è qui mostrato:
void int_net(NN *rete, FILE *weight_file,BOOLEAN np)
La funzione free_net invece libera la memoria dalle variabili della struttura
precedentemente allocate con build_net.
Prima di introdurre le due procedure responsabili dell’addestramento della rete, forwardf
e backwardf, sulle quali è interessante operare un confronto con le corrispondenti
funzioni Matlab forward e backward, ricordiamo la presenza di alcune funzioni
di utilità, quali print_weight per visualizzare i pesi della rete, save_state
o save_weights per memorizzare l’intera struttura o soltanto i pesi della rete,
extract per l’estrazione casuale di un numero.
Forwardf riceve una rete già inizializzata, un vettore degli inputs ed un vettore degli
outputs: applica alla rete, quale ingresso, il vettore double degli inputs e calcola la
corrispondente uscita, copiandola quindi nel vettore degli outputs. Il suo prototipo è qundi
il seguente:
void forwardf (NN *rete, VET_DB inputs, VET_DB *outputs)
Per ogni neurone q del livello s, dapprima viene calcolato l’ingresso pesato
totale (3.11), quindi la sua uscita (3.12) attraverso la funzione neu_function, al cui
interno troviamo un’istruzione “case” sul tipo di funzione di attivazione (scelto fra le
logsig, tansig, radbas e purelin precedentemente descritte,
anche se tale insieme può venire facilmente esteso). Al termine del processo, quando si raggiunge
l’ultimo livello della rete, risultano aggiornati l’ingresso z e l’uscita y di
ogni neurone.
A parte la gestione delle variabili puntatore, l’uso continuo di cicli “for” annidati (per
calcolare gli ingressi pesati totali e le corrispondenti uscite di ogni neurone) e la necessità
di costruire/richiamare manualmente le funzioni di attivazione (in Matlab, oltre ad essere già
disponibili, venivano applicate semplicemente attraverso l’operatore feval), non si
notano grandi differenze in merito alle “difficoltà” e ai tempi implementativi rispetto alla
corrispondente forward di Matlab.
Tutte queste “complicazioni” del C incidono, invece, in maniera determinante sullo sviluppo di
backwardf. Essa è responsabile dell’aggiornamento dell’intera rete, ovvero di compiere
un passo di discesa nello spazio dei pesi attraverso l’algoritmo del gradiente.
A tale scopo, riceve in ingresso la rete già inizializzata, i vettori delle derivate parziali
della funzione di costo rispetto agli ingressi della rete e alle uscite dell’ultimo livello,
oltre naturalmente alla variabile 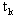 che
definisce la lunghezza del passo di discesa (abbiamo visto che essa è esprimibile in funzione
del passo di addestramento k come
che
definisce la lunghezza del passo di discesa (abbiamo visto che essa è esprimibile in funzione
del passo di addestramento k come 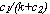 ,
dove
,
dove 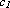 e
e
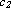 sono costanti che caratterizzano
il problema).
sono costanti che caratterizzano
il problema).
La chiamata alla funzione backwardf si rifà al seguente prototipo:
void backwardf (NN *rete, VET_DB *dJy0, VET_DB dJyL, double tk)
dove 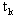 è la lunghezza del passo di discesa,
dJyL il vettore delle derivate parziali della funzione di costo rispetto alle uscite dell’ultimo
strato, mentre dJy0 quello rispetto agli ingressi della rete.
è la lunghezza del passo di discesa,
dJyL il vettore delle derivate parziali della funzione di costo rispetto alle uscite dell’ultimo
strato, mentre dJy0 quello rispetto agli ingressi della rete.
Possiamo ora brevemente riassumere i fattori che hanno rallentato la codifica in C della
“fase backward” della back-propagation:
· allocazione dinamica per le 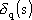
· impiego di variabili temporanee per memorizzare le 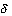 dei livelli s e s+1
dei livelli s e s+1
· uso “massiccio” di cicli “for” annidati per calcolare le
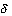 di ogni neurone, le derivate parziali
della funzione di costo rispetto al singolo peso e per aggiornare di conseguenza il suo valore
di ogni neurone, le derivate parziali
della funzione di costo rispetto al singolo peso e per aggiornare di conseguenza il suo valore
· implementazione delle derivate delle funzioni di attivazione (dlogsig, dtansig,
dradbas e dpurelin).
Rispetto alla versione in Matlab, ad esempio, il calcolo delle
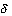 risulta essere assai meno “immediato”,
come possiamo notare dalle seguenti righe che ne codificano l’algoritmo:
risulta essere assai meno “immediato”,
come possiamo notare dalle seguenti righe che ne codificano l’algoritmo:
for (p=1; p<=(qn->n).vet[s]; p++)
{ delta_new.vet[p] = 0.0 ;
if (s==qn->livelli) delta_new.vet[p] = delta.vet[p] ;
else
for (q=1; q<=(qn->n).vet[s+1]; q++)
delta_new.vet[p] += delta.vet[q] * (qn->net[s+1][q].w).vet[p] ;
delta_new.vet[p] *= dfunzatt(qn->net[s][p].z,(qn->tipo_fa).vet[s]) ;
}
3.5 Librerie a disposizione
Saranno qui riassunte e brevemente elencate le principali funzioni implementate in Matlab e in C,
capaci nel loro insieme di fornire all’utente uno strumento per lo sviluppo di applicativi
sulle reti neurali.
In Matlab, come abbiamo visto, per gestire l’intero ciclo di vita di una rete neurale sono
sufficienti le seguenti funzioni:
· buildnet (costruttore della rete)
· initnet (inizializzazione casuale dei pesi)
· forward (fase forward della back-propagation)
· backward (fase backward della back-propagation).
Al contrario, in C, si sono dovute implementare molte procedure di supporto alle funzioni
strettamente necessarie per il modello e ciò ha condotto alla realizzazione delle seguenti
librerie:
· neu_def.h (funzioni di attivazione logsig, tansig, radbas
e purelin, con rispettive derivate dlogsig, dtansig, dradbas
e dpurelin)
· neu_mem.h (funzioni per l’allocazione dinamica di matrici e vettori con elementi
interi/reali, quali mat_i_allc_ini, mat_d_allc_ini, vet_i_allc_ini,
vet_l_allc_ini, vet_d_allc_in, mat_d_free, mat_i_free,
vet_d_free, vet_i_free, vet_l_free; per l’allocazione dinamica
dei neuroni, come nalloc e de_nalloc, o delle reti neurali, quali
ralloc e de_ralloc)
· neu_kern.h (funzioni per costruire/ripulire una rete, come build_net e
free_net, funzione per inizializzarla init_net, funzioni per il suo
addestramento, quali forwardf e backwardf, funzioni di interfaccia con
il file system, come save_state, save_weights, loadnet)
· neu_uti.h (funzioni per l’estrazione casuale dei numeri, come rnd o
extract, funzioni per la gestione degli errori, funzioni per l’inizializzazione
casuale di vettori/matrici e insiemi di vettori/ matrici, come vet_d_init o
set_vet_d_init).

Ringraziamenti,
Introduzione,
Capitolo 1,
Capitolo 2,
Capitolo 3,
Capitolo 4,
Bibliografia

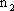 è la dimensione della funzione da
approssimare,
è la dimensione della funzione da
approssimare, 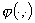 è una data funzione base,
mentre i
è una data funzione base,
mentre i 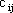 e le componenti di
e le componenti di
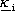 sono i parametri da determinare,
esprimibili anche come unico vettore
sono i parametri da determinare,
esprimibili anche come unico vettore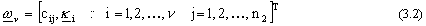
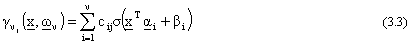





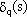 sono calcolate “a ritroso” per
mezzo della (3.9)
sono calcolate “a ritroso” per
mezzo della (3.9)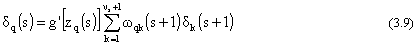
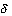 sia l’algoritmo del gradiente per
l’aggiornamento dei pesi, dal momento che l’ambiente consente di chiamare le funzioni anche
su argomenti strutturati (vettori, matrici o cell-array).
sia l’algoritmo del gradiente per
l’aggiornamento dei pesi, dal momento che l’ambiente consente di chiamare le funzioni anche
su argomenti strutturati (vettori, matrici o cell-array).
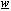 .
.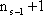 scalari double, ovvero gli
scalari double, ovvero gli
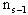 pesi sulle uscite del livello precedente
s-1, oltre al bias, e quindi sarà esprimibile come:
pesi sulle uscite del livello precedente
s-1, oltre al bias, e quindi sarà esprimibile come: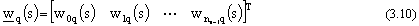
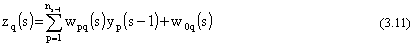

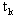 che
definisce la lunghezza del passo di discesa (abbiamo visto che essa è esprimibile in funzione
del passo di addestramento k come
che
definisce la lunghezza del passo di discesa (abbiamo visto che essa è esprimibile in funzione
del passo di addestramento k come 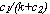 ,
dove
,
dove 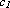 e
e
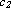 sono costanti che caratterizzano
il problema).
sono costanti che caratterizzano
il problema).